Спасибо! Попробую обосновать то, что Вы написали.
Поскольку

1) то при

найдутся такие

и

, при которых для всех

и

будет

2) а при

либо найдутся такие

и

, при которых для всех

и

будет

а для остальных

и

будет

либо для всех

и

и для всех

и

будет

что в общем дает

Вижу, что у меня получилось такое же сложное рассуждение как и сначала (вернее, то же самое рассуждение несколько другими словами), но, наверное, если "рассматривать возможности оторванные от действительности", то есть если рассматривать не только неравенства, но и неактуальные здесь равенства, то просто и не получится? Хотя у
Odysseus получилось гораздо проще, чем у меня (меня даже поразило, насколько проще):

быть не может ни для каких

, так как

это наименьшая из верхних границ

А это и есть все доказательство, поскольку если

неверно, то

Вопрос
А зачем рассматривать "возможности оторванные от действительности"?
очевидно, можно перенаправить Фихтенгольцу, это ведь он рассматривает неактуальные здесь равенства. Я бы доказывал по другому:
Из

следует

и

отсюда

таким образом имеем два класса рациональных чисел: нижний класс

и верхний класс

.
Элементы класса

ограничивают класс

сверху, а элементы класса

ограничивают класс

снизу, поэтому имеется точная верхняя граница
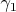
класса

и точная нижняя граница
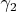
класса

.
При этом класс

не имеет наибольшего числа, а класс

не имеет наименьшего, так что разность

Цитата:
может быть сделана сколь угодно малой.
А тогда, по лемме 2, существует только одно число, содержащееся между суммами

и

(Фихтенгольц, там же.)
То есть

(обозначим это число

).
Между прочим, так заодно было бы доказано и существование, и единственность числа

Должен, все-таки сказать, что лично для меня это и хорошо, что Фихтенгольц ведет читателя таким трудным для (моего) понимания путем -- мне было очень полезно пройти по нему.
К тому же в лемме 2 (
https://studfile.net/preview/4422204/page:3/ стр.21) также употребляются неактуальные здесь равенства.



