Тут вот что надо учесть. Даже если физическая система идеально сферически симметрична (например, одна неподвижная частичка), для её описания можно выбрать неподходящую систему координат. Например, какие-нибудь
сфероидальные координаты. В них интервал уже не будет иметь тот вид, что у Дирака. Да что там сфероидальные, достаточно взять обычные сферические координаты, но центр поместить не там, где находится частичка. Так что система координат должна соответствовать симметрии системы.
Например, пока не могу понять: куда деваются угловые множители:

;

...?
Для простоты будем говорить об искривлённом трёхмерном пространстве. Если в нём введена система координат

, то в каждой точке

определён локальный координатный базис из векторов
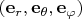
или, короче,

. В другой точке — другой базис, так что точнее было бы писать

, но не хочется загромождать запись.
Каждый из базисных векторов

в точке

касателен к «своей» координатной линии, то есть кривой, которая получится, если стать в

, а затем начать менять координату

, остальные сохраняя неизменными. Например, вектор
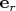
в точке

касателен к координатной линии

, проходящей через

. Базисные векторы в общем случае не являются ни единичными, ни ортогональными друг другу.
Существует соотношение между базисными векторами

и компонентами метрического тензора в той же точке:

Итак, если в любой точке базисные векторы ортогональны друг другу, матрица

в любой точке будет диагональной.
В выражении для

коэффициент перед множителем

— это компонента

(точнее, ещё с множителем

). Если она равна нулю, соответствующее слагаемое в развёрнутой сумме не пишут. Если она не равна нулю, это значит, что

, то есть векторы

и
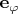
неортогональны. А это означает, что обозначения

создают только видимость сферической системы, но на самом деле СК нарушает сферическую симметрию: «радиальная» координатная линия

образует непрямой угол со сферой, проходящей через точку

и с центром в начале координат.