Добрый день. Помогите разобраться с решением данной задачи.
У меня есть две абсолютно одинаковые кастрюли с круглыми донышками. В каждом донышке просверлено одинаковое число абсолютно одинаковых отверстий. Только в первой кастрюле все отверстия достаточно далеко отстоят друг от друга, а во второй, наоборот, образуют одну плотную группу. (Достаточно далеко - значит, что расстояния между отверстиями намного больше диаметра отверстий. Плотная группа, наоборот, означает, что расстояния между отверстиями в несколько раз меньше диаметра отверстий.)
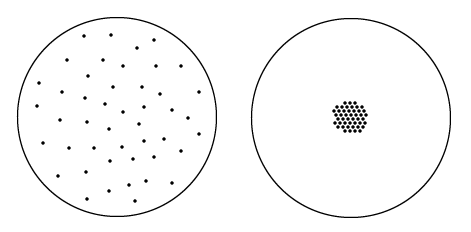
Теперь я наливаю в обе кастрюли одинаковый объем воды.
Вопрос 1. Эта вода вытечет из обеих кастрюль за одинаковое время или нет?
Вопрос 2. Если время будет разным, значит на скорость вытекания воды влияет расположения отверстий. Тогда каким физическим законом описывается эта зависимость?
Мне кажется, что я когда-то читал о том, что если группа отверстий расположена близко друг к другу, то их можно считать одним большим отверстием. Но я не могу ничего найти об этом законе.
Может кто-то помочь решить эту задачу?



