k= 1:289117532242004794657842939580523992192206081574833651083505729789364385249494747835588176048973824211799073812844695893338800
k= 2:700807927515209319703919656110904985720190564273728927174449393318844544118832456311147693474287827223544034590280514266879002491356850375432550518244301303196
k= 3:1104328042755954386320824567216377485763072493389864968788783627789917668277472692529025908780612163573893802542538816626102673973609068657811347934560841187329583701473956
k= 4:147074933269000430744730232888347281954754442423944038651420598928646041661597978060547563153220821207473952363371199598114353577172981806080972506876322789924495061432074210008
k= 5:30411808902652962586922105368190882705618102801009965823210890366003342948804331065813223236122586004662523653525648565692496030820301476522766621402751077196480252433600351153719
k= 6:347755923814266600087641996025482293071765314357120818677434698385772606400923265457843065007263143733323810942246434251114523849066507676339505260704260597474486272370233614578025
k= 7:897035112429980066950886430172585529641880706166863688853610486891124891861145297478069715246826966432638884313647796652292853154029319921243531674741482012482020986013900386006423
k= 8:1037509359853699222040353323704397314138432215441528828639057443671479731266891734834513499947748012166213012827161776163176869972745620508504930918585570242412029417780826633293177
k= 9:790386659931054161018560953395902682409839816179057191828066843229019020955589488910645561846788652240648589258080285685236562007488091388739578817539677394011672471007730088222855
k=10:487290342914887567428268511868035526656860026750957159447842643023559362907340024708997514622334574306716359108584612841571947409512289005908806999351222667496516301012058231344997
k=11:270212370245824109525880386625616244419136746555055568186534012918165267431685075373760635060656140402154628091932677261316034777201297207291301759966817452516688201145234276433339
k=12:142125204153675917427277447640626050100633446822547466245321639996481621514925162082809280157672080111385130501957996420347138940213342137807411188205494146445796146775778645471712
k=13:72813512208775219553727472775524630674212436409612012408075499664237249718806701391113105809542530959304970540713367770404446481973869601929612981320978067697971892293827186417745
k=14:36818717372373582792083664785126123020650317495237734239578845912770100831212089383723392572464268949439791583470330616330710337578114063116409204104835980693673497355280428619439
k=15:18496838427342109535636893493783811856324684140304453218076263462836839454431902728956911984357243762717253408227412013983840953724033283300552115706277645729324911178137445626624



 бросках появится отрезок одинаковых букв длины
бросках появится отрезок одинаковых букв длины  (в тексте
(в тексте  ). Но что-то достаточно простого решения не просматривается (может, просто устала к концу недели
). Но что-то достаточно простого решения не просматривается (может, просто устала к концу недели  , а хотя бы
, а хотя бы  бросков.
бросков.





 .
. . То есть для
. То есть для  бросков.
бросков. .
. (вероятности выпадения всех строк короче
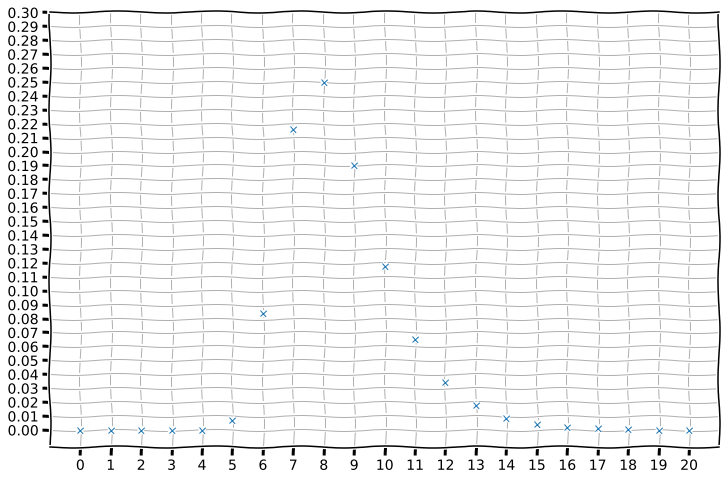
(вероятности выпадения всех строк короче  , не так уж мало. Интересно почему у Вас получилось 38 из миллиона и 0 из ста тысяч.
, не так уж мало. Интересно почему у Вас получилось 38 из миллиона и 0 из ста тысяч. это вероятность получить длиннейшую подстроку длиной ровно
это вероятность получить длиннейшую подстроку длиной ровно  ?
? .
.
 взял от
взял от  и всех
и всех  , и она равна
, и она равна  , где
, где  берётся из
берётся из  :
:  ,
,  ,
,  ,
,  ,
,  ,
,  ,
,  ,
,  ,
,  ,
,  ,
,  ,
,  ,
,  .
. ).
). и
и  , что явно выбивается из вероятностей, с артефактами генератора случайных чисел при прогонах у
, что явно выбивается из вероятностей, с артефактами генератора случайных чисел при прогонах у 
 , ...,
, ...,  ?
? :
: и для
и для  , с
, с  совпадает с Вашими
совпадает с Вашими  (упс, тут походу кто-то промахнулся ...).
(упс, тут походу кто-то промахнулся ...). бросков брать
бросков брать  , то вероятность невыпадения ни орлов ни решек для
, то вероятность невыпадения ни орлов ни решек для  будет
будет  , вдвое меньше, но всё равно
, вдвое меньше, но всё равно  совсем не мало, а числители:
совсем не мало, а числители: ?
? , ...,
, ...,  Свои значения я привёл. У Вас какие значения вероятностей получились?
Свои значения я привёл. У Вас какие значения вероятностей получились? вообще, ни удвоенных, никаких. Плюс тут
вообще, ни удвоенных, никаких. Плюс тут  вместо
вместо  (100,010,001,101). Значит наверное неправильная.
(100,010,001,101). Значит наверное неправильная. разберём:
разберём:



 .
. - тоже совпадает после удвоения.
- тоже совпадает после удвоения. :
:




 из
из