Назовем примарными элементами множества элементы, которые сами не являются множествами
Такие элементы обычно называются атомами. Иногда их удобно иметь, но тогда их совокупность нужно определить. В стандартных теориях множеств, таких, как ZFC или NBG, атомов нет, и все элементы являются множествами, а все множества являются элементами. При этом ничего не теряется, а всё, что можно сделать в теории с атомами, можно сделать и без них.
В современной математике множества, являющиеся элементами самих себя, "запрещены" (вводится специальная аксиома, говорящая, что они не существуют). Запрещены, в частности, потому, что чреваты парадоксами.
Ну нет, причина "запрета" совсем другая. Дело в том, что если у нас теория противоречивая, то нельзя избавиться от противоречий, добавляя новые аксиомы: новая аксиома — это дополнительное средство доказательства, и всё, что можно доказать без неё, можно доказать и с ней (просто не употребляйте её). Причиной противоречий в первоначальной "наивной" теории множеств был так называемый неограниченный принцип свёртывания Фреге, который утверждал, что каждое свойство определяет множество элементов, обладающих этим свойством. В ZFC этого принципа, естественно, нет, а вместо него есть аксиома выделения и более сильная аксиома подстановки (другое название — аксиома замены; конечно, она сильнее не принципа Фреге, а аксиомы выделения, и была введена позже аксиомы выделения, поскольку та оказалась недостаточной для формализации некоторых стандартных математических рассуждений).
Множества, являющиеся собственными элементами, запрещены аксиомой регулярности (другое название — аксиома фундирования): если

— непустое множество, то существует такой элемент

, что

. Появилась она заметно позже других аксиом, и, разумеется, не для того, чтобы запретить множеству быть своим элементом. Просто она полезна для доказательств, и "устройство" множеств с этой аксиомой выглядит более упорядоченным, а множества, принадлежащие "самому себе", как будто бы никому не нужны. Во всяком случае, я не слышал ни о каких содержательных применениях таких множеств. Разумеется, если кому-нибудь такие множества понадобятся — ради бога. Выкидывайте аксиому регулярности (вместе со всеми опирающимися на неё теоремами) и изучайте. Но построить такое множество, используя остальные аксиомы теории множеств, невозможно, так что существование множества, удовлетворяющего условию

, нужно просто принять за аксиому.
Все аксиомы ZFC "выводятся" из представления о том, что все множества можно построить "по шагам".
Первоначально у нас ничего нет, поэтому на первом шаге мы можем построить только пустое множество

. На втором шаге у нас есть один элемент
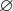
, поэтому мы можем построить множество

. На третьем шаге у нас есть два элемента
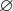
и

, и мы можем построить ещё некоторые множества. И так далее.
Перед каждым шагом у нас есть совокупность уже выполненных шагов. На новом шаге мы можем построить всевозможные множества из тех элементов, которые были построены на предыдущих шагах (включая сюда и множества, построенные на предшествующих шагах).
Вообще говоря, не для каждой совокупности шагов следует шаг "после" всех этих шагов. Но мы можем считать, что такой шаг заведомо существует в следующих случаях:
1) совокупность состоит из одного шага (не обязательно первого);
2) совокупность шагов представляет собой бесконечную последовательность, занумерованную всеми натуральными числами;
3) у нас есть некоторое (уже построенное) множество

, для каждого

существует некоторый (уже выполненный) шаг

, и совокупность шагов состоит из всех шагов

,

.
Например, то, что множество не может быть своим элементом, следует просто из того, что элементы множества должны быть построены раньше самого множества, поэтому в момент построения множества оно ещё не существует и не может быть использовано в качестве элемента.
Но это всё неформализуемо, и является просто "философским" обоснованием аксиом ZFC.
В формальном виде существует очень похожая конструкция доказательства совместности аксиомы регулярности и аксиомы выбора с остальными аксиомами. Пусть имеется некоторая модель теории ZF без аксиомы регулярности и аксиомы выбора. Внутри этой модели строится новая модель, в которой аксиома регулярности и аксиома выбора справедливы.
Построение происходит по шагам. Роль шагов играют ординалы (они могут быть определены и построены без аксиомы регулярности и аксиомы выбора).
На нулевом шаге у нас ничего нет, и мы можем определить только пустое множество. Это означает, что мы можем записать формулу, определяющую множество, но участвующие в этой формуле переменные пробегают не все элементы исходной модели, а только те, которые к этому шагу определены. Перед нулевым шагом у нас ещё ничего не определено, поэтому ничего, кроме пустого множества определить нельзя.
На последующих шагах происходит то же самое: на очередном шаге мы определяем новые множества, используя те, которые были определены на предыдущих шагах, и конструкция проходит по всем ординалам, имеющимся в исходной модели.
Совокупность всех определённых таким образом множеств (они называются конструктивными; на мой взгляд, название неудачное, так как вызывает ложные ассоциации с конструктивной математикой, но можно было бы использовать термин "определимые") удовлетворяет всем аксиомам ZFC, включая аксиому регулярности и аксиому выбора. Кроме того, в этой модели выполняется очень сильная аксиома конструктивности V=L, которая утверждает, что все множества конструктивны. И, как сюрприз, в этой модели верна обобщённая гипотеза континуума, которая утверждает, что для каждого бесконечного кардинала

между

и

нет промежуточных кардиналов. Обобщённая континуум-гипотеза сама по себе является очень сильным утверждением. Например, из неё выводится аксиома выбора.
P.S. Как я вижу,
Vladimir Pliassov усиленно подталкивает тему к псевдофилософским умствованиям на околоматематические темы, регулярно "забывая" то, что ему объясняли ранее. Он явно не является тем, за кого себя выдаёт, поскольку иногда проговаривается, демонстрируя знакомство с достаточно нетривиальными вопросами. Почтенной публике это не надоело?