Здесь я буду задавать наивные вопросы по теории вероятностей. Вопросы задаются по одному, следующий после закрытия предыдущего.
Вопрос № 1. Строгое определение системы случайных величин.Наивное описание случайной величины. Случайная величина принимает то или иное значение в результате случайного опыта ("броска кубика").
Строгое определение случайной величины. Рассмотрим множество элементарных исходов

с заданной на нём сигма-алгеброй событий

и вероятностной мерой

- другими словами, вероятностное пространство

. Рассмотрим также пространство

с заданной на нем сигма-алгеброй

(обычно в качестве

выступает

или некоторое его подмножество). Случайной величиной

называется

-измеримая функция
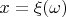
, определенная на

и принимающая значения из

.
Перевод строгого определения на человеческий язык. Каждый раз, когда в результате опыта появляется тот или иной элементарный исход

, случайная величина

принимает значение

, однозначно определённое этим элементарным исходом:
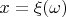
. Мы можем говорить о вероятности того, что

примет значения из некоторого подмножества

, и все имеющие вероятность подмножества

образуют сигма-алгебру

. Вероятность того, что

примет значение из

, есть вероятность события

(которое по условию

-измеримости функции

таки событие, т.е. принадлежит

и, следовательно, имеет вероятность).
Наивное описание системы случайных величин. Если в результате случайного опыта принимают свои значения несколько случайных величин (например, координаты выбранной точки), говорят, что они образуют систему. Принципиально важно, что все случайные величины в системе принимают значения в результате одного и того же опыта ("броска кубика"), так как только в этом случае с несколькими случайными величинами можно выполнять осмысленные действия (складывать их, считать корреляционный момент и так далее).
Строгое определение системы случайных величин. К сожалению, не нашёл ни в одном учебнике, который просматривал.
Вопрос: как оно формулируется? Верно ли, что система из двух случайных величин

предполагает одно вероятностное пространство

и одну сигма-алгебру

на

, но две

-измеримых функции

,

определенные на

и принимающие значения из

?
Теоретически можно было бы рассмотреть на

отдельные сигма-алгебры

и

для случайных величин

, входящих в одну систему. Но т.к. обычно ограничиваются рассмотрением борелевских подмножеств

, то в таком усложнении, по-моему, нет особого смысла.
Ещё можно было бы взять одно и то же множество элементарных исходов

с заданной на нём одной сигма-алгеброй событий

, но разные вероятностные меры

и тем самым получить разные вероятностные пространства

и

. Но не теряется ли при этом интуитивный смысл объединения случайных величин в систему? Если случайный опыт состоит, скажем, в выборе точки на плоскости, а случайные величины в системе - её координаты, то каждая точка плоскости - элементарный исход, события - подмножества плоскости, и каждому событию приписана только одна вероятность.
Дополнительный вопрос, связанный с первым. Случайная величина называется непосредственно заданной, если

,

и

. Если я правильно формулирую определение системы случайных величин, то непосредственно заданная случайная величина может образовывать систему только с самой собой. Это так?



