Пусть
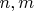
— натуральные числа,


то есть множество векторов из нулей и единиц, содержащих в точности

единиц. Пусть линейный оператор

(со стандартным базисом в

) удовлетворяет условию: если

то

то есть

является инвариантным множеством оператора

Мне нужно выяснить, следует ли тогда отсюда, что матрица

есть матрица перестановки.
Мои попытки решения задачи. Возьмём два вектора

и

из

с единицами на местах

и

соответственно. Обозначим


Тогда


Вычитая

из

получаем, что

это верно для любых

от 1 до

в силу произвольности

Значит, элементы любой

-й строки матрицы

имеют вид

либо

Кроме того, имеем:


Вычитая, получаем

для всех индексов

Так как при сложении

таких сумм должно получиться

то каждая такая сумма должна равняться единице:

для любого индекса

то есть сумма любого столбца матрицы

равна единице.
Но вот что делать дальше - я не знаю, у меня тупик. Помогите пожалуйста разобраться.