Вот еще кое-что.
Винберг, стр.138 писал(а):
Итак, мы можем утверждать, что

Для того чтобы найти коэффициенты

и

, будем придавать в этом равенстве переменным
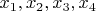
какие-нибудь выбранные значения. Представим вычисления в виде таблицы, в правом столбце которой будем выписывать получаемые уравнения:

Таким образом,

и

, так что

На этом месте надо читать между строк. Если я все правильно помню, Винберг вводит многочлен

над произвольным полем. И над произвольным же полем он его выражает через элементарные симметрические

. Но мне кажется, что так делать нельзя. В процессе решения этого примера есть деление на

, но никто не обещал, что

. Правильнее наверное было бы сделать пометку, что рассуждения выше справедливы не для любого поля. Ну или можно просто сказать, что здесь мы ограничимся рассмотрением

или

.
-- 30.04.2021, 14:05 --Ну и в любом случае, даже если я промахнулся с делением, там все равно мы пытаемся решить СЛАУ с 2 неизвестными. При данных наборах

и

(если мы решаем задачу над произвольным полем), ее матрица коэффициентов не всегда будет невырожденная. Так что все равно решать этот пример над произвольным полем не очень корректно.



