Мне нужна помощь уважаемых математиков форума. Имеется следующее разложение искомой функции в степенной ряд:

где коэффициенты

для любого
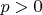
. C физической точки зрения данная модельная функция описывает, согласно теории Ландау, тейлоровское разложение свободной энергии

термодинамической системы в ряд по параметру порядка

вблизи точки фазового перехода первого рода, который достигается путем увеличения давления

при фиксированной температуре

для веществ с аномальной зависимостью температуры плавления от давления (ее понижению с ростом

). Особенности этой функции следующие. При

имеется локальный минимум. При больших значениях

данная функция неограниченно возрастает. При относительно небольших значениях

имеется глобальный минимум, соответствующий точке

Мне необходимо чтобы этот минимум "двигался вправо и вверх", проходя через нуль и становясь локальным минимумом (т.е. переставая быть глобальным минимумом). Я выяснил, что при увеличении коэффициентов

и

этот глобальный минимум движется вверх и влево, тогда как при увеличении

он сдвигается вниз и вправо. Пытался выбирать различные функциональные зависимости этих коэффициентов от параметра

для смещения вправо и вверх но увы..... Основное требование к этим зависимостям-они должны быть по-возможности проще (линейные функции, константы). Чувствую, должен быть какой-то наработанный регулярный метод такого поиска функциональных зависимостей.



