"Простая" в смысле менее точная и более понятная и удобная человеку.
Самым точным будет скорее всего указание типа/вида и величины погрешности. Например абсолютная

. Или относительная

. А ещё часто применяется относительная от верхнего предела некоей величины (шкалы прибора или диапазона представимых чисел или диапазона нормализованных чисел с одинаковой величиной показателя).
А точность в три знака не указывает ни на абсолютную погрешность, ни на относительную (с некоторыми оговорками), зато человеку очень даже понятно что число с точностью в три знака

отличается от точного значения менее чем на
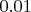
(а часто и менее чем на

, зависит от соглашения).
Связаны же они произведением, для точности в

знаков погрешность (относительная от верхнего предела) составит

или

. Т.е. если понимать точность в

знаков как представимость чисел до

, то произведение точности

и погрешности (указанного типа)

даст

. Фактически видя погрешность

можно сразу сказать что точность составляет

"верных" знаков (верных в смысле см.выше, могут и отличаться, но не более чем на единицу младшей значащей цифры). На самом деле объяснять дольше чем показать на примерах.
Изредка применяется и не целая точность, например

знака как в компьютерном формате single, в таком случае она понимается как (десятичный) логарифм отношения максимального возможного значения представимого числа к его минимальному представимому приращению (без изменения порядка в экспоненциальном представлении) (собственно так точность и определяется). Например если числа представлены как целые до

с шагом

единиц, то точность составит

знаков, не три и не два. Иногда это важно, и что максимальное число не состоит из всех девяток, и/или что шаг не обязательно равен единице младшего разряда. Ещё пример, в двоичной системе, число из 8 битов имеет точность

десятичных знака, независимо от положения десятичной или двоичной точки, хоть

, хоть

, хоть

(запись в двоичной системе).
PS. Обращу внимание что в метрологии (и более обще в математике) погрешность понимается гораздо более строго и больше их типов, как выше правильно указано. Я говорю лишь о вычислительных приложениях.