[Дописано к предыдущему посту.]
(То есть если мы берём условный курс аффинной геометрии, там скорее всего отрезок
![$[A; B]$ $[A; B]$](https://dxdy-03.korotkov.co.uk/f/6/b/9/6b9fdd12129d7987f4498e3146e0bfeb82.png)
будет определяться как множество

— прям как у вас спрашивается в задаче. На худой конец, как множество
![$\{ A + m \overrightarrow{A B} : m \in [0; 1] \}$ $\{ A + m \overrightarrow{A B} : m \in [0; 1] \}$](https://dxdy-02.korotkov.co.uk/f/1/d/7/1d745fb4232d31d4479a11b97b83e67e82.png)
, но такое определение не совсем хорошо видимой несимметричностью. Впрочем, могут быть и более описательные определения, например какое-нибудь «единственное ограниченное пересечение лучей, исходящих из

и из

, лежащих на прямой

» — вот тут уже будет совсем немного нетривиального доказательства, но потребуется определить ограниченность без связи с метрикой, которой в аффинном пространстве над упорядоченным полем (упорядоченность вот точно нужна, иначе мы сможем рисовать только прямые) быть не обязательно — например как вхождение в какой-нибудь симплекс.)
Это задача 1.12 из задачника по Лин.Алгебре Беклемишева. Я так понимаю, что в ней надо показать, что никакие другие вектора не лежат на этом отрезке.
Хм, хорошо, ну у меня его сейчас нет под рукой, может кто-то лучше с ним знаком; всё-таки было бы хорошо знать, что там говорится про отрезки где-нибудь рядом, если найдётся и несложно выписать…
Пока всё в точности не ясно, можно попробовать показать, что если на этом отрезке лежит что-то ещё, то получится как минимум треугольник, но по-моему ерунда выходит. Можно показать, что он лежит целиком на прямой

, но вроде там особо нечего показывать, т. к. по условию линейная комбинация — аффинная, ровно такая, какими задают аффинные подпространства.

Останется разве что показать одномерность.
-- Пн мар 01, 2021 04:07:32 --А, но и ещё ведь осталась интересная задача: в каком отношении точка

делит
![$[a; b]$ $[a; b]$](https://dxdy-01.korotkov.co.uk/f/8/a/7/8a7e884ac3e21fa78b571d4ab33fd88682.png)
. Опять же это зависит от определений, но возьмём например такое: отрезки
![$[S_1; S_2]$ $[S_1; S_2]$](https://dxdy-02.korotkov.co.uk/f/d/f/5/df50e4643365e4d447a12fa5064ad0fd82.png)
и
![$[T_1; T_2]$ $[T_1; T_2]$](https://dxdy-02.korotkov.co.uk/f/d/6/b/d6b79f793693b3624f9657cd0dc3c0a882.png)
параллельны ровно тогда, когда найдутся числа
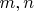
такие, что

, и имеют в таком случае отношение длин

(справа модули чисел). Тогда всё просто получится.



