Наши нет, но если мы возьмём треугольник со сторонами

, то результаты будут ровно те же. Впрочем ниже этот совет никак не применён:
(Следующее писалось параллельно.)
Обозначим центр окружности

и пересечём
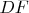
с перпендикулярной ей

в

(середине
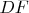
), аналогично на

нарисуем

и на

нарисуем

. Мы видим например что

а те площади равны половинам
![$[AO] \cdot [DF], [BO] \cdot [DE], [CO] \cdot [EF]$ $[AO] \cdot [DF], [BO] \cdot [DE], [CO] \cdot [EF]$](https://dxdy-02.korotkov.co.uk/f/5/0/1/501069f7218876fea6e014911767d19682.png)
соответственно. Как-то у вас должно вывестись, что
![$[AO] \cdot [A'O] = [BO] \cdot [B'O] = [CO] \cdot [C'O]$ $[AO] \cdot [A'O] = [BO] \cdot [B'O] = [CO] \cdot [C'O]$](https://dxdy-04.korotkov.co.uk/f/7/3/1/7310121a561470af6794f1d8c106e2f782.png)
— это квадрат радиуса окружности (привет от инверсии). Мы можем также сказать

а эти-то слагаемые в свою очередь равны полвинам
![$[A'O] \cdot [DF], [B'O] \cdot [DE], [C'O] \cdot [EF]$ $[A'O] \cdot [DF], [B'O] \cdot [DE], [C'O] \cdot [EF]$](https://dxdy-02.korotkov.co.uk/f/1/9/7/197fb0be43f80d91ecc245249afcad6782.png)
.
Казалось бы, ещё немного покрутить и всё откроется. Как на деле — не знаю, я просто поиздевался над треугольником в GeoGebra.
UPD: добавил квадратных скобок дабы идти в ногу с исходным постом.



