Здравствуйте. Время от времени у меня возникают математические "парадоксы". Сейчас думаю над следующим.
Есть две функции

и

. Во второй функции под интегралом будем понимать первообразную, величина

это параметр. Далее, есть производные этих функций

и

.
Пусть

, тогда заменим корень

.
Тогда
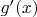
стремиться к

при

. Делее, если подставить выражения для корня под интеграл и проинтегрировать, то

будет стремиться к

при

.
Но, если в Mathematica ввести интеграл

и получить первообразную через эллиптический интеграл первого рода, а потом построить графики функций

и

при различных значениях параметра

, то виходит, что

стремится к

при меньшем значении

, а при большем наоборот больше отходит от функции

. Это первое непонятное место.
И ещё, если построить график, например,

, то на графике наблюдаются осцилляции, тем больше, чем больше параметр

. Второе непонятное место.
Также я видел что-то о связи между эллиптическим интегралом и гипергеометрической функцией, как думаете, может лучше с ней работать, или в данном примере это ничего не изменит?
Не знал, нужно ли приводить здесь код в Mathematica и графики, если это окажется нужным, то приведу.



