Хотел бы высказать некоторые соображения по вопросам, которые часто поднимались как на этом форуме, так и в принципе являются довольно популярными:
1) Можно ли доказать теорему Кантора (мощность любого множества меньше, чем мощность множества его подмножеств) только от противного?
2) (Когда признается, что есть и прямой метод) Являются ли прямые способы этого доказательства более простыми и логичными?
Ответ на второй вопрос может быть субъективным, но на этом форуме было так много тем с вопросами о данной теореме, и значение этой теоремы в математике настолько велико, что, как минимум, стоит рассмотреть и альтернативные доказательства.
Наиболее популярное доказательство теоремы Кантора использует предположение о наличии биекции (или сюрьекции, чего в данном случае достаточно)

, из которого затем выводится противоречие. Практически во всех русскоязычных учебниках которые я видел, а также в
русскоязычной и
англоязычной Википедии, оно звучит примерно следующим образом:
Теорема Кантора. Для произвольного множества

и множества всех его подмножеств

верно
 Стандартное доказательство от противного.
Стандартное доказательство от противного. Во-первых, существует инъекция, сопоставляющая каждому элементу
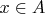
одноэлементное подмножество

, значит

Теперь рассмотрим отображение

и построим множество

, состоящее из всех элементов

, не принадлежащих своим образам при отображении

.
Предположим, что  это сюръекция. Тогда существует
это сюръекция. Тогда существует  такой, что
такой, что  .
.Далее в обоих случаях возникают противоречия:
- Если

, то поскольку

, должно быть

, но тогда по определению

,

- Если

, то поскольку

, должно быть

, но тогда по определению

,

Следовательно, предположение о наличии сюръекции ложно, и значит

С этим доказательством, как мне кажется, есть ряд проблем:
1. В нем используется доказательство от противного без которого, на самом деле, можно обойтись (что часто предпочтительнее). Это уже не раз обсуждалось на этом форуме, последний раз в
Доказательство теоремы о мощности множества подмножеств.
2. Конструкция "если

, то ...

, а если

, то ...

", хотя и достаточная для доказательства, не кажется слишком прозрачной. Возникает аналогия (пусть и неверная, но психологически близкая) с брадобреем, который бреет всех кроме самого себя, с парадоксом лжеца и т.д. Как минимум, не очень хорошо понимаешь "что здесь происходит". Теорема доказалась и ложки нашлись, но осадок остался.
3. Диагональный метод Кантора, который он придумал впервые для доказательства именно этой теоремы, при таком методе доказательства довольно завуалирован. Для сравнения, при доказательстве того, что

он используется более явно: для любого отображения

по диагонали строится вещественное число, которое не совпадает ни с каким образом при данном отображении. Иногда при этом тоже говорят "предположим, что существует сюръекция", но в данном случае эти слова точно лишние.
Главная проблема здесь в конструкции противоречия из п.2. Если использовать ее, то
приходится доказывать от противного, поскольку сам аргумент этой конструкции заключается в сведении к противоречию. А чтобы доказывать не от противного, то конструкция главного аргумента должна быть другой.
Есть другой метод доказательства, который я встречал только в двух источниках: оригинальное доказательство Кантора в его "Трудах по теории множеств" (статья "Об одном элементарном вопросе учения о многообразиях", стр. 170-171) и оно же, но в более современных терминах, у Александрова во "Введении в теорию множеств и общую топологию" (глава 1, § 6, теоремы 15 и 16). В них вместо множества всех подмножеств

рассматривается множество всех отображений

. Конечно, при этом доказывается то же самое, поскольку мощность последнего равна мощности

, но ход доказательства несколько другой. При этом намного более явно используется диагональный метод Кантора, и все доказательство практически идентично доказательству того, что

(если ограничиться вещественными числами на интервале
![$[0, 1]$ $[0, 1]$](https://dxdy-03.korotkov.co.uk/f/e/8/8/e88c070a4a52572ef1d5792a341c090082.png)
записанными в двоичной системе счисления, далее я эту оговорку уже не повторяю). Единственная разница будет в том, что множество

может быть несчетным, но это в сути доказательства ничего не меняет.
Подозреваю, что составителю большинства учебников этот метод доказательства теоремы Кантора не нравится потому, что формально он более длинный. Однако логически и "визуально" он настолько же простой как и доказательство

с которым, вроде, ни у кого проблем нет.
ОДНАКО, и стандартное доказательство можно немного модифицировать так, чтобы 1) не было необходимости доказывать от противного и 2) доказательство стало несколько проще и яснее, и не использовало рефлексивных конструкций "если

, то ...

, а если

, то ...

". Эта модификация элементарна, поэтому я уверен, что где-то она приводится. Но лично я ее не встречал, поэтому опишу ее ниже (как прямое доказательство под номером 1, поскольку оно по конструкции ближе к стандартному методу). После этого приведу также оригинальный вариант доказательства Кантора (под номером 2) и в нем буду приводить параллели с прямым доказательством #1 и с доказательством

, которые мне кажется тоже будут полезны.
Прямое доказательство #1 (модификация стандартного доказательства). Первая часть такая же, как и в доказательстве выше от противного. Существует инъекция сопоставляющая каждому элементу
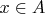
одноэлементное подмножество

, значит

Далее, тоже как и раньше, рассмотрим отображение

и множество

.
Но теперь не будем предполагать, что  это сюръекция, т.е. не будем предполагать, что существует
это сюръекция, т.е. не будем предполагать, что существует  такой, что
такой, что 
Вместо этого сразу напрямую покажем, что не существует

такого, что

.
- Если

, то по определению

,

, значит

.
- Если

, то по определению

,

, и значит тоже

.
Значит

это не сюръекция. С учетом произвольности

, сюръекции между

и

не существует вообще, значит

---
Также приведу терминологию и визуальный прием, которые помогают мне представить эти импликации на таком уровне, что они становятся еще более естественными и интуитивными. Возможно, кто-то еще найдет эти образы полезными.
- Подмножество

назовем "своим" для элемента

, если

принадлежит этому подмножеству. Элемент назовем "верным" (относительно отображения

), если при отображении

он переходит в свое подмножество, т.е. для верных элементов

.
- Аналогично, подмножество назовем "чужим" для элемента

, если

не принадлежит этому подмножеству. Элемент назовем "неверным", если при отображении

он переходит в чужое подмножество, т.е. для неверных элементов

.
- Очевидно, что любой элемент или верный, или неверный.
- Теперь можно просто описать словами почему в

не переходит ни один из элементов

. Подмножество

состоит только из неверных элементов, значит туда не могут переходить верные элементы (поскольку не встретят там себя). И при этом в
 все
все неверные элементы, значит туда не могут переходить неверные элементы (поскольку встретят там себя).
- Я при этом также представляю верные элементы зеленым цветом, а неверные - красным. Зеленые могут переходить только в те подмножества, где есть хотя бы один зеленый элемент. А красные не могут переходят в подмножества где есть все красные элементы. А значит в подмножество

где есть все красные и ни одного зеленого - никто переходить не может.
- Еще может быть, когда у данного  красных элементов нет вообще, например когда это описанная выше инъекция из
красных элементов нет вообще, например когда это описанная выше инъекция из  в одноэлементные подмножества
в одноэлементные подмножества  . Тогда
. Тогда  это пустое множество и все зеленые элементы в него тоже не могут переходить.
это пустое множество и все зеленые элементы в него тоже не могут переходить.
- Кодирование разных элементов цветами, диаграммами и формами мне было полезно и в других ситуациях. ИМХО это хорошо стимулирует ассоциации и привыкание к новым понятиям.Другой визуальный прием напрямую связан со вторым методом прямого доказательства описанным ниже. В нем элементы уже не разбиваются на "верные" и "неверные", и даже не разбиваются на группы

или

, а просто для каждого элемента

по отдельности доказывается, что он не может перейти в

.
----
Прямое доказательство #2 (более явное использование диагонального метода Кантора).Это доказательство несколько длиннее, но построение здесь "более конструктивное" и практически такое же, как и при стандартном доказательстве диагональным методом

Поэтому идеологически оно не менее простое, чем первое.
Сначала напомним известное доказательство того, что мощность

равна мощности множества отображений

. Здесь все очевидно: каждому отображению

соответствует разбиение

на два непересекающиеся подмножества:

и

. Рассматривая

как характеристическую функцию подмножества
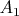
, выделяющую его из

, можно сказать, что каждому

соответствует какое-то подмножество

и наоборот.
Значит далее можно сравнивать

не с

, а с мощностью множества характеристических функций на

, которое будем далее обозначать как

. Но для того, чтобы проводить параллели с предыдущим прямым доказательством полезно все время держать в голове как каждая характеристическая функция связана с ее подмножеством

, т.е. мы не отказываемся от картинок подмножеств, а просто переводим эти картинки "на алгебраический язык". (Я буду ниже приводить мелким шрифтом такие параллели, а также параллели с доказательством

)
Через

будем обозначать

, через

- конкретную функцию из

, которая в силу этого соответствия отвечает элементу

, а через

- значение этой функции на элементе

. Это главные понятия, которые нужно понять в данном доказательстве, после этого все строится уже автоматически.
- При доказательстве  , аналогом
, аналогом  будет конкретная инъекция
будет конкретная инъекция  , аналогом
, аналогом  - вещественное число в которое переходит натуральное число
- вещественное число в которое переходит натуральное число  , а
, а  - разряд этого числа под номером
- разряд этого числа под номером  .
.
- В случае подмножеств, аналогом  будут отображение
будут отображение  , аналогом
, аналогом  - подмножество, в которое переходит элемент
- подмножество, в которое переходит элемент  , а
, а  - характеристикой того, входит ли элемент
- характеристикой того, входит ли элемент  в это подмножество: если
в это подмножество: если  , то входит, а если
, то входит, а если  , то не входит.
, то не входит.Наличие инъективности

очевидно как и в предыдущих методах доказательства. Для каждого элемента

построим

таким образом, что

и


.
- В случае подмножеств, аналогом будет сопоставление каждому элементу 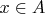 одноэлементного подмножества
одноэлементного подмножества  .
.Теперь, как и в первом прямом доказательстве, рассмотрим произвольное отображение

и докажем, что оно не может быть сюръективным. Т.е. докажем, что существует функция

, которая не равна ни одному

.
- При доказательстве  , аналогом будет построение вещественного числа, в которое не переходит ни одно натуральное.
, аналогом будет построение вещественного числа, в которое не переходит ни одно натуральное.
- В случае подмножеств, аналогом будет построение подмножества, в которое не переходит ни один элемент  .
.Построим такую функцию

по следующему правило:

, т.е. если

, то

и если

, то
 - При доказательстве
- При доказательстве  , аналогом будет построение по диагонали вещественного числа, которое в каждом разряде
, аналогом будет построение по диагонали вещественного числа, которое в каждом разряде  отличается от образа соответствующего натурального числа
отличается от образа соответствующего натурального числа  в этом разряде.
в этом разряде.
- В случае подмножеств, аналогом будет построения подмножества  , поскольку те элементы, которые принадлежат своему образу мы в него не включаем (меняем в них
, поскольку те элементы, которые принадлежат своему образу мы в него не включаем (меняем в них  на
на  ), а те, которые не принадлежат своему образу - включаем (меняем в них
), а те, которые не принадлежат своему образу - включаем (меняем в них  на
на  ).
).И теперь, даже проще чем в первом прямом доказательстве, видно, что


, поскольку их значения отличаются на элементе

:

.
- При доказательстве  , будет полный аналог.
, будет полный аналог.
- В случае подмножеств, аналогом будет доказательство того, что в  не переходит ни один элемент
не переходит ни один элемент  поскольку все элементы там "неверные".
поскольку все элементы там "неверные". Получилось в итоге довольно длинно, но, мне кажется, достаточно прозрачно и может заслуживать внимания с методической точки зрения.
Выводы (все ИМХО)- Наиболее популярное доказательство теоремы Кантора использует метод доказательства от противного, без которого можно обойтись за счет небольшой модификации этого доказательства. Кроме того, прямое доказательство будет использовать более ясную конструкцию для главного аргумента, чем конструкция из противоречий в стандартном доказательстве от противного.
-- Для дополнительных аналогий кому-то может быть также полезна предложенная выше терминология "своих/чужих" множеств и "верных/неверных" элементов вместе с их цветовой маркировкой, но это уже дело вкуса.
- Есть еще одно прямое доказательство (оригинальное доказательство Кантора), которое более явно использует диагональный метод. По свой логике, оно очень близко как к доказательству того, что

, так и к прямому доказательству полученному модификацией стандартного доказательства от противного.
- Оба прямых доказательства, как минимум, заслуживают упоминаний как альтернативные методы (намного большего, чем у них есть сейчас). Возможно даже, одно из них должно рассматриваться как основной метод доказательства по сравнению с текущим стандартным методом. Для тех, кто будет предпочитать более короткий способ - можно использовать прямое доказательство #1, близкое к стандартному. Для тех, кто будет предпочитать лучше понять логику диагональному метода и связи этого доказательства с

- можно использовать прямое доказательство #2.



