Если фиксировать число
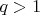
, то для любого положительного числа

найдется и притом единственное целое число

такое, что

Не понимаю момент в доказательстве.
Сначала проверяется, что множество чисел вида

, не ограничено сверху. Потом, что для любого числа

найдется такое натуральное число

, что при любом натуральном

будет

. Следовательно для любого числа

найдется число

такое, что при всех натуральных

будет

.
И сразу же утверждается, что

ограничено снизу. Не понимаю как связать ограниченность с предыдущими предложениями.



