Получается, внутрь направлена.
Ну да внутрь направлена.
Это кстати следует, из выведенной Вами формулы:
Так как
а) с одного края соленоида: при движении (по силовой линии поля) от края внутрь соленоида напряженность магнитного поля растет, то

имеет положительный знак, а значит
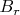
- отрицательный, то есть направлена к оси

б) с другого конца соленоида - при движении (по силовой линии поля) изнутри к краю соленоида напряженность магнитного поля падает, то

имеет отрицательный знак, а значит
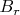
- положительный, то есть направлена от оси

.
-- 05.11.2020, 22:39 --Теперь к первому вопросу.
а) У Вас получилось верно: если кольцо находится на оси в такой области пространства, что в какой-то момент времени

направлена вверх, а

направлена от оси, то и средняя сила действующая на кольцо будет направлена вверх. Вот только это будет у верхнего края соленоида, а не у нижнего, как в условиях.
б) Аналогично, если кольцо находится на оси в такой области пространства, что в какой-то момент времени

направлена вверх, а

направлена к оси, то средняя сила действующая на кольцо будет направлена вниз.
В общем случае - кольцо отталкивается от соленоида.
Подозреваю, что правильный ответ у Вас получился почти случайно - просто Вы обращали внимание на формулы для величин, но не на знаки. Хорошо бы, чтобы Вы отследили знаки, и убедились, что в пункте а) действительно знак у средней силы получает плюс (что она направлено в направлении

, которая направлена вверх).
Для этого нужно проверить:
1. Какое направление тока в кольце считается положительным?
2. Какой знак получается в выражении для тока перед синусом?
4. Какой знак имеет векторное произведение для силы Ампера? Без учета знака сдвига фазы
3. Какой знак имеет сдвиг фазы?
Вроде бы ничего не забыл.