A cylindrical solenoid with an iron core, of cross-section radius

, is placed vertically on a
table. A thin metallic toroidal ring, of inner radius

, is placed around the lower end of the coil, so
that the inner circumference of the ring is in contact with the surface of the coil. The resistance of
the ring is

, its mass is

and its inductance is

.
The solenoid is connected to an alternating voltage source of angular frequency

. This
leads to a vertical, homogenous, sinusoidally oscillating magnetic field of amplitude inside the
coil
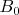
; its orientation is such that, at

(i. e. at the initial time), it points upwards (along the axis
that I will further denote by

). Apart from this, the finite length of the solenoid leads to a radial,
horizontal, oscillating magnetic field, of amplitude
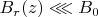
which depends only on the height

from the base of the coil and with an orientation such that, at

, it points outwards.
It turns out that, if the magnetic field is strong enough, the ring will start floating.
(a) What is the value of
for which the ring will float at a constant height?
Remark: The oscillations of the magnetic field are fast enough for the motion of the ring during a
single period of oscillation to be insignificant.
Привел оригинал текста задачи, а то иногда есть определенная путаница из за моего перевода.
Моя попытка решения заключается в следующем:
Индукция магнитного поля на оси катушки будут
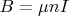
где
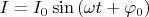
,
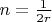
, что спорно, ибо так мы пренебрегаем конечными размерами катушки.
Полное сопротивление катушки будет
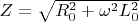
где
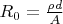
сопротивление катушки (пусть у нее будет высота
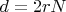
,

- число витков)
Так-же, можем использовать закон сохранения потока вектора индукции магнитного поля.
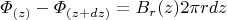
Пока что не могу понять в каком направлении двигаться дальше для решения задачи.