Разность натуральных чисел по индукции

[VoprosT]

Требуется по индукции доказать следующее утверждение (упражнение из Зорича): $((m,n \in \mathbb{N}) \wedge (m<n))\Rightarrow((n-m) \in \mathbb{N})$
По какой букве тут надо вести индукцию?По $m$? Или отдельно по $n$ и $m$, как это делается при док-ве для суммы?

Я попробовал вести индукцию по $m$.
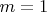
Для $m = 1$ утверждение доказано (это было выше по тексту в Зориче - у любого натурального $n>1$ есть предыдущий элемент)
Но во время перехода к $m+1$ появляется возможность $m+1 = n$ (а это не удовлетворяет условию), и я не очень понимаю, как это строго обговорить.

UPD: Кажется, понял. Если $m+1 = n$, то мы не смотрим на нашу импликацию, потому что она тогда уже нас заведомо не интересует(потому что на самом деле доказываем по индукции утверждение вида: $(((m,n \in \mathbb{N}) \wedge (m<n))\Rightarrow((n-m) \in \mathbb{N})) \vee (m \geqslant n)$ , а если $m+1 < n$, то переход осуществляется в общем-то очевидно. Подскажите, пожалуйста, правильные ли у меня рассуждения?

[Lia]

VoprosT
Считаете, что по $m$ -- попробуйте, посмотрите, спросите, если не получится. Считаете, что по $n$ -- тоже. Ну и т.д. Это и называется попытками решения.

[Lia]

Тема перемещена из форума «Помогите решить / разобраться (М)» в форум «Карантин»
по следующим причинам:


- отсутствуют собственные содержательные попытки решения задач(и).

Исправьте все Ваши ошибки и сообщите об этом в теме Сообщение в карантине исправлено.
Настоятельно рекомендуется ознакомиться с темами Что такое карантин и что нужно делать, чтобы там оказаться и Правила научного форума.

[Lia]

Тема перемещена из форума «Карантин» в форум «Помогите решить / разобраться (М)»