В анализе Зорича в 5-ом упражнении к третьему параграфу первой главы(издание 2020, стр. 22) предлагается доказать эквивалентность следующих утверждений относительно отображения


:
а)

инъективно;
b)

c)

;
d)

e)

, если

Я решил доказать последовательно импликации от первого к последнему и потом замкнуть e)

a), но столкнулся с некоторыми проблемами:
1. В упражнении 3.b) доказывается
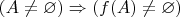
. Правильно ли я понимаю, что верно и обратное? Потому что тогда

, и с помощью этого факта я доказываю импликацию c)

d).
2. Возникают трудности с переходом от d) к e). Если B - пусто, тогда всё очевидно вытекает из d), а если нет, то я не понимаю, как осуществить шаг.
Подскажите, как быть



