Движущийся наклонный стержень (СТО)

[misha.physics]

Здравствуйте.
В механике Иродова есть такая задача: В $K$-системе есть неподвижый стержень длины $l$ под углом $\alpha$ к оси $Ox$. Найти его длину $l'$ и угол $\beta$ в $K'$-системе, движущейся относительно $K$-системы со скоростью $V$ вдоль $Ox$. Рисунок из книги



В книге задача решается так: $l'=\sqrt{(\Delta x')^2+(\Delta y')^2}$, $\tg{\beta}=\Delta y'/{\Delta x'}$, $\Delta y'=\Delta y$, $\Delta x'=\Delta x\sqrt{1-V^2/c^2}$.

На первый взгляд воспринимается очевидным, но потом эта очевидность у меня пропала, так как все-таки здесь мы применяем формулы сокращения длины для проекции и хотелось бы понять это более обстоятельно. Я сделал рисунок



Здесь $AO$ положение стержня в $K$-системе, $BO$ положение стержня в $K'$-системе, $OC=\Delta y=\Delta y'$, $AC=\Delta x$, $BC=\Delta x'$, $\Delta x'=\Delta x\sqrt{1-V^2/c^2}$. Из треугольников получаем $BC/AC=EF/DF=\Delta x'/{\Delta x}=\sqrt{1-V^2/c^2}$, где $AC\parallel DF$. Вроде получается как в книге. Но для этого нужно чтобы точка $A$ стремилась к $B$, точка $D$ к $E$, то есть чтобы $AO$ стремился к $BO$, это и есть наши стержни. Но здесь получается так, что точки стержня $AO$ перемещаются вправо на прямую $BO$, то есть "длины сокращаются как бы вправо". А почему так происходит? 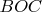Вот заменим стержень $AO$ на треугольную пластину $AOC$, тогда в $K'$-системе мы будем видеть пластину $BOC$, но почему прямая $OC$ будет перпендикулярной и в $K$- и в $K'$-системах? 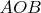Почему например пластинка $AOC$ не перейдет в пластину $AOB$ (в смысле, по форме, понятно что отрезки там будут другими, нужно будет чтобы $AC=\Delta x$, $AB=\Delta x'$)? Из одного закона сокращения длины я не могу ответить на эти вопросы.

P.S. Кстати, подскажите, пожалуйста, как называется свойство или теорема для треугольников, что $BC/AC=EF/DF$, а то я "увидел" что это как бы верно, но не могу вспомнить как это называется или как получить. Похоже на теорему Фалеса, но вроде другое. Или все-таки из нее выводиться?

[svv]

Положим стержень в плоскую прямоугольную коробку, так, чтобы он был её диагональю. Так яснее?

[Pphantom]

А еще лучше - рассмотрим вместо стержня координаты его концов и вспомним, что "сокращение масштабов" - это подсчет изменения разности координат по оси, которая совпадает с направлением относительной скорости СО.

[misha.physics]

Спасибо, так яснее, и с коробкой и с координатами (действительно ещё лучше). Я что-то извилистой дорогой пошёл, хотел проследить как меняются длины всех отрезков типа $AC$, $DF$ и т.д., но не понимал как эти изменения взаимосвязаны. Значит удобнее представить себе сплюснутую координатную сетку вдоль $Ox$ равномерно вдоль $Oy$. Значит стержень ненулевой толщины будет сокращаться вот так



и $A'=A$, $a'=a$, $B/B'=b/b'=\sqrt{1-V^2/c^2}$ (здесь стержень неподвижный в $K'$, так привычнее).

[Eule_A]

misha.physics
А Вы в учебник самого Иродова не заглядывали? Там часть, касающаяся СТО, неплоха вполне. А для практики я бы Вам ещё посоветовал в задачник под редакцией Сивухина заглянуть. Там хорошие задачи.

[misha.physics]

Eule_A в сообщении #1474398 писал(а):

А Вы в учебник самого Иродова не заглядывали? Там часть, касающаяся СТО, неплоха вполне.

Да, начальная задача из этого учебника. И теорию я там с самого начало перечитываю. Спасибо за задачник.

[Eule_A]

Чуть не забыл.

misha.physics в сообщении #1474377 писал(а):

но не могу вспомнить как это называется или как получить

Просто через подобие треугольников.

[misha.physics]

Спасибо. Доказал с помощью $OCA\sim OFD$ и $OCB\sim OFE$.