System of equations from an old magazine

[nnosipov]

Several students, not all my students, of course. To the problems: unfortunately, the variant with "an errata" is too complicated technically. At the moment, I don't know how it can be simplified. (I need to the so-called resultant technique, but this is no so good, I prefer more popular ideas.) Thus, the problem has "сырая формулировка" (sorry, I don't know how one can say this phrase in english).

[ins-]

For the initial system is valid the following geometric interpretation: "Это пересечение трёх поверхностей (двухмерных) в трехмерном пространстве. Решением может быть и не тройка чисел (то есть поверхности могут не пересекаться по одной-единственной точке."

[ins-]

Thanks to Rak so dna and Wolfram Alpha finally solved it: https://artofproblemsolving.com/communi ... 2p16511713 and collected more solutions you may like.

[Pphantom]

ins- в сообщении #1474375 писал(а):

Thanks to @Rak so dna and Wolfram Alpha

ins-, click on his nickname to mention the participant, please. The result will be something like Rak so dna.

[nnosipov]

nnosipov в сообщении #1474354 писал(а):

At the moment, I don't know how it can be simplified.

Well, the following "corrupted" system can be proposed as an exam task with the "reasonable" answer:

$$2+(y-z)^2-2x=17+(x-z)^2-8y=81+(y-x)^2-18z=0.$$

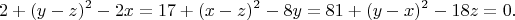
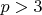
The difference from the original system is that now we have the coefficients $2$ and $17$ instead of $1$ and $16$, correspondly. The problem can be formulated as: find the number of solutions over $\mathbb{F}_p$ for an arbitrary prime $p>3$. The required (expected) answer must be given explicitly: this means that the primes $p$ for which we have the same number of solutions must be desribed explicitly (for examle: those primes have the form ...).

[ins-]

It will be interesting to share the results from this exam.

I found more interesting systems. They'd be probably very easy for the most of users here, but I'll share them. It is one of the systems: topic141828.html

In the past I also created some "corrupted" systems. You can see some of them:

$x+xy+\frac{1}{xyz}=2$
$\frac{1}{y}+\frac{1}{yz}+\frac{1}{xyz}=3$
$\frac{1}{z}+\frac{1}{zx}+\frac{1}{xyz}=4$

$\frac{1}{x}+\frac{1}{y-z}=\frac{2}{3}$
$\frac{1}{y}+\frac{1}{z-x}=\frac{3}{4}$
$\frac{1}{z}+\frac{1}{x-y}=\frac{4}{5}$

$\frac{1}{x}+\frac{2}{y-z}=\frac{1}{2}$
$\frac{3}{y}+\frac{1}{z-x}=\frac{1}{3}$
$\frac{1}{z}+\frac{4}{x-y}=\frac{1}{4}$

The last two were modifications of:

$\frac{1}{x}+\frac{1}{y+z}=\frac{1}{2}$
$\frac{1}{y}+\frac{1}{z+x}=\frac{1}{3}$
$\frac{1}{z}+\frac{1}{x+y}=\frac{1}{4}$

[nnosipov]

Generally speaking, the Groebner's basis technique can kill it easily, I think (and the exotic case of finite fields is assumed, too). So those examples can be useful for ... what? I see only one way: for the olympiad tasks where we can operate only elementary methods.

[ins-]

nnosipov в сообщении #1475288 писал(а):

So those examples can be useful for ... what? I see only one way: for the olympiad tasks where we can operate only elementary methods.

Yes, it is the idea. I have no dedicated math education. A long time ago I faced similar olympiad problems and I liked them. Sometimes as a hobby I solve and create problems.