Пусть
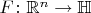
все также липшицево отображение. Пусть в

задано дифференциальное уравнение

с глобально липшицевым векторным полем

. Тогда

расслаивается на полные траектории этого дифференциального уравнения. Можно ли доказать, что для почти всех

для соответствующей полной траектории

с

функция

будет дифференцируемой в

для почти всех

?
Кажется, что в данном случае тоже достаточно аргумента типа Фубини: нужно использовать тот факт, что

дифференцируема почти везде на

(теорема Радемахера). Дальше доказывать, что если борелевское подмножество

имеет меру нуль, то для почти всех

пересечение

с траекторией, начинающейся из

, имеет одномерную хаусдорфову меру нуль.
Заметим, что в другую сторону это неверно: например, для

.
В нужную нам сторону похоже на правду. Но я не знаю, как это быстро доказать. Грубо говоря, в тех точках, где

, это тривиально (траектории сами являются точками). Если
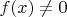
, то локально должна быть какая-то теорема о выпрямлении, но я точно не знаю, какая именно в ней нужна гладкость. Может и липшицевости достаточно.
Мне кажется, что верно следующее:
Возьмём

такое, что

, и в точке

нарисуем гиперплоскость, перпендикулярную

. Тогда существует окрестность

точки

в этой гиперплоскости и

, такое что решение уравнения даёт билипшицев гомеоморфизм между некоторой окрестностью точки

в

и множеством

. Если так, то из этого всё будет следовать.
Конечно, конечным числом таких окрестностей не обойтись, но счётным можно, и для вопросов множеств меры нуль этого должно быть достаточно.



