Вступительная в CS center

[vatrushka]

Собственно, задача:
Последовательность $x_n$ задается условием $x_0 = b$ , $x_{4n + 4} =x_{4n+3}= \sqrt{a\cdot \frac{x_n + a}{2}}, x_{4n + 1} = x_{4n + 2} = \frac{2x_n + a}{3}$ Имеет ли эта последовательность предел?
($b>a>0$)
Что я сделал:
Сперва, я записал, что если она и имеет предел $t$, то $t = \sqrt{a\cdot \frac{t + a}{2}}$, и $t = \frac{2t + a}{3}$, решая это уравнение, получим $t =a$ и $t = a, t = -\frac{1}{2}$
Таким образом, если предел и есть , то он равен $a$.

Далее я сравнил $\sqrt{a\cdot \frac{x_n + a}{2}}$ и $\frac{2x_n + a}{3}$
Первое больше второго при $t>a$
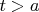
Назову $f_1(t)$ - пропускание $t$ через первую формулу, а $f_2(t)$ - пропускание t через вторую формулу.
Можно показать что если $a<t<b$, то и $a<f_1(t)<b$ и $a<f_2(t)<b$.
Дальше начинаются тонкие моменты
Ясно что при пропускании через такую формулу $t$ раз получится что наибольшее число получится при $f_1(f_1(f_1(t)))$ , а наименьшее при $f_2(f_2(f_2(t)))$. Дальше можно показать что предел $f_1(f_1(f_1(t)))$ равен $a, -\frac{a}{2}$, через первую - $a$.
Понятно, что $-\frac{a}{2}$- не подходит.
Теперь надо как то применить наверное теорему о двух миллиционерах, но я не очень понимаю как это акуратно сделать
Спасибо.

[vpb]

Ни при чем тут два полицейских. Докажите, что для любого $t>a$ как $f_1(t)$, так и $f_2(t)$ лежит к $a$ ближе, чем $t$ (это если я сам на этот счет не ошибся, конечно).

[vatrushka]

Ну допустим правда, следующее ближе чем предыдущее, и что?
Это не доказательство существования предела

[VoprosT]

По существу у вас две последовательности, разность между которыми бесконечно мала, достаточно показать, что одна(по факту - обе) из них ограничена и монотонна

[vpb]

А, ну то есть вы моим предложением о том, куда вам направить свою мысль, недовольны, и ждете от меня обоснования целесообразности данного предложения ?

[vatrushka]

vpb в сообщении #1469863 писал(а):

А, ну то есть вы моим предложением о том, куда вам направить свою мысль, недовольны, и ждете от меня обоснования целесообразности данного предложения ?

Нет, вы не правы, я доказал этот факт
Не очень понятно что он дает.....

-- 20.06.2020, 22:12 --

VoprosT в сообщении #1469862 писал(а):

По существу у вас две последовательности, разность между которыми бесконечно мала, достаточно показать, что одна(по факту - обе) из них ограничена и монотонна

Это то я как раз доказал

Вопрос в другом

как из того что $f_1(f_1(f_1(.....)$ и $f_2(f_2(f_2(.....)$ стремятся к одному и тому же числу следует сходимость исходной последовательности?

-- 20.06.2020, 22:22 --

Я это немного опустил, но да, если $t>a$, то $\frac{2t+a}{3} > a$, но $t > \frac{2t + a}{3}$
И аналогично если $t>a$, то $t>\sqrt{a\frac{t+a}{2}}> a$
То-есть последовательность $f_1(f_1(.....))$ и $f_2(f_2(f_2(.....)))$ убывает и ограниченна снизу значит имеет предел
А что дальше?)

[VoprosT]

vatrushka в сообщении #1469812 писал(а):

Далее я сравнил $\sqrt{a\cdot \frac{x_n + a}{2}}$ и $\frac{2x_n + a}{3}$
Первое больше второго при $t>a$

Разве не наоборот?
Потом просто показываете ограниченность и монотонность $\frac{2x_n + a}{3}$, ограниченность другой последовательности тоже пригодится(хватит того,что она ограничена снизу числом $a$). Вот вам и теорема о двух милиционерах.

Ещё можно заранее доказать, что $x_n>a$, и не накладывать условие $t>a$, когда выясняете, как соотносятся две посл-ти

[vatrushka]

VoprosT в сообщении #1469875 писал(а):

vatrushka в сообщении #1469812 писал(а):

Далее я сравнил $\sqrt{a\cdot \frac{x_n + a}{2}}$ и $\frac{2x_n + a}{3}$
Первое больше второго при $t>a$

Разве не наоборот?
Потом просто показываете ограниченность и монотонность $\frac{2x_n + a}{3}$, ограниченность другой последовательности тоже пригодится(хватит того,что она ограничена снизу числом $a$). Вот вам и теорема о двух милиционерах.

И при док-ве можно оперировать просто тем, что $x_n>a$ , а не $t>a$

Да, вы правы
Вопрос в другом.
Можно представить это в виде двоичного дерева, где переход влево будет означать переход по $f_1$, а вправо - по $f_2$. Ну вот мы доказали что идя от корня все время влево или все время вправо мы получим конкретный предел и они равны.
И как это связанно со сходимостью исходной последовательности?
(как я понимаю можно считать что переход идет только в $n \to 2n + 1$ и $n \to 2n + 2$

[VoprosT]

Надеюсь,меня поправят,если я ошибаюсь, и заранее извиняюсь,если моё решение неправильное(потому что уже и сам начал сомневаться после момента с деревом,который сам,честно говоря,объяснить не могу,поэтому и извиняюсь за качество ответа, возможно, мне вообще не стоило пытаться помочь)
Мы знаем, что наши две посл-ти порознь стремятся к одному и тому же числу. А наша исходная посл-ть выглядит вот так: $x_0,x_1,x_2,x_3,x_4,...,x_{4n+1},x_{4n+2},x_{4n+3},x_{4n+4},x_{4n+5},x_{4n+6},x_{4n+7},x_{4n+8},...$ (перемешанные члены тех двух посл-ей), тогда мы можем $\forall\varepsilon>0$ найти $N=\max(N_1,N_2)$:$\forall n>N$ верно $\left\lvert{x_n-a}\right\rvert<\varepsilon$

[vatrushka]

Так в том то и прикол, что если бы это были просто перемешанные $f_1, f_1(f_1()), f_1(f_1(f_1()))$ и $f_2, f_2(f_2()), f_2(f_2(f_2()))$ тогда да, все хорошо, но тут же не так,
в последовательности например есть еще $f_1(f_2(f_1()))$, и это непонятно как обработать .

[vatrushka]

Я вот доказал собственно еще что $a<f_1(t) < t$, $a<f_2(t) < t$, то-есть получается что каждая ветка дерева имеет предел.
Теперь надо бы возможно доказать что предел каждой из веток равен $a$
Есть какие то идеи?
То есть как не чередуй $f_1$ и $f_2$ в пределе будет одно и то - же
Есть у кого то идеи?

[adfg]

vatrushka
оцените приращение каждой из функций. Производные обеих функций в конце концов посчитайте, если уж совсем тупняк в голове. Там же не просто всё к $a$ стремится, там со скоростью геометрической прогрессии туда стремится

[vatrushka]

Так, я еще смог доказать что если $-\varepsilon < t - a< \varepsilon$, то $\varepsilon < f_1(t) - a< \varepsilon$ и $-\varepsilon < f_2(t) - a< \varepsilon$

[VoprosT]

Актуальным остаётся вопрос vatrushka о том, что делать с членами последовательности, вида f_1(f_2(f_1))) и т.п. В Фихтенгольце видел подобную задачу, там устремляли $n$ к бесконечности отдельно по чётным и нечётным номерам, но там вроде и в рекуррентном соотношении было отдельно указано,что чётные зависят от чётных, а нечётные от нечётных. А что делать тут?

(Оффтоп)

P.s. за предыдущий оффтоп извиняюсь, поправил.

[kotenok gav]

VoprosT в сообщении #1470903 писал(а):

Сообщение, чтобы набрать классы и поднять тему.

И получить замечание за исскуственный подъем темы?