На примере этой картинки хотелось бы разобрать основные понятия, как я их понимаю:
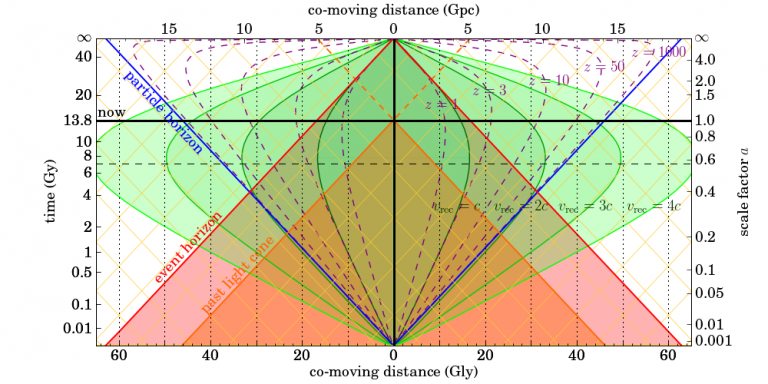
Здесь изображена эволюция нашей Вселенной согласно модели

, но все понятия приложимы и к моделям Фридмана.
Это конформное отображение пространственно-временной плоскости, т.е. световые конусы в разных точках плоскости различаются только масштабом. Следовательно, пути световых лучей такие же, как в плоском пространстве-времени Минковского: прямые с наклоном 45 градусов.
По горизонтали отложены сопутствующие координаты, т.е. координатная сетка, растущая вместе с расширением пространства. Любой объект во Вселенной в любой момент времени имеет одни и те же неизменные сопутствующие координаты.
Справа по вертикали отложен масштабный фактор, умножив на который сопутствующую координату объекта можно получить мгновенное расстояние до объекта (расстояние вдоль прямой

). Т.к. масштабный фактор растет со временем, неизменные сопутствующие координаты объекта с течением времени означают все большее расстояние до него. Значения сопутствующих координат выбраны такими, чтобы масштабный фактор в настоящее время был равен 1.
Слева по вертикали отложено космологическое координатное время, т.е. время на часах наблюдателей с постоянной сопутствующей координатой.
Нижняя горизонтальная прямая соответствует моменту большого взрыва, верхняя горизонтальная прямая - в данном случае временной бесконечности. Линия now отмечает настоящее время (13,8 млрд.лет). Диаграмма неограниченно продолжается в обе стороны.
Все события, находящиеся за пределами светового конуса прошлого, построенного из точки нашего текущего расположения (оранжевый) мы пока не наблюдаем. Снизу этот конус упирается в момент

- начало мировых линий обьектов во Вселенной - и есть много мировых линий галактик, которые он пока не покрыл ни в одной точке. Эти галактики находятся для нас в настоящее время за пределами горизонта частиц (синий) - мы еще не видели ни одного момента из их жизни. (Галактик в начале мировых линий еще не было, но для простоты будем говорить так).
С течением времени основание светового конуса расширяется, покрывая (начиная с начала) все большее число мировых линий галактик. Но на приведенной картинке видно, что световой конус прошлого, даже построенный из временной бесконечности (красный), не покрывает всей плоскости, а у многих мировых линий не покрывает ни одной точки. Периметр светового конуса прошлого, построенного из временной бесконечности - это горизонт событий. Точек событий вне этого конуса мы никогда не увидим. В частности, мировые линии объектов, находящихся от нас сейчас за пределами

млрд.св.лет для нас не наблюдаемы ни в одной своей точке, т.е. мы никогда не увидим ни одного момента из их жизни.
В открытых вселенных Фридмана конформное отображение не ограничено сверху, т.е. там световой конус прошлого рано или поздно покроет любую точку событий на любой мировой линии, горизонт событий отсутствует.
Пунктирные линии - линии постоянного красного смещения

. Закон Хаббла говорит о пропорциональности между мгновенным расстоянием до галактики (вдоль прямой

) и ее красным смещением

. В этом масштабе такая пропорциональность скорее отсутствует. Она наблюдается, как можно здесь видеть, только в узком диапазоне, примерно до

(т.е. только до красного смещения, соответствующего увеличению длины волны света вдвое.). Т.к.

для объектов, находящихся на горизонте частиц, бесконечно, а сам горизонт удален от нас в любой момент времени на конечное расстояние (в данный момент - на 45 млрд.св.лет согласно рисунку), то закон Хаббла не может быть точным для всех наблюдаемых галактик. При приближении объектов к горизонту частиц закон Хаббла сильно завышает расстояние до них.
Во нашей Вселенной бесконечное число галактик, но мы увидим лишь конечное их число за все время своей жизни. Мы будем постоянно наблюдать начало жизни новых объектов на удаляющемся горизонте частиц все дальше и дальше от себя, но темп их появления будет все ниже и ниже. Появление последнего из конечного числа доступных нам для наблюдения объектов мы увидим через бесконечное время на бесконечном от нас удалении. В то время мы с полным правом сможем сказать, что обозреваем бесконечную Вселенную, хотя она по прежнему будет составлять малую часть того, что существует.
Правильно ли я понимаю это?



