Alexey RodionovВ математической энциклопедии есть статья
Лакунарный степенной ряд, в которой приведена такая
Теорема (Адамара о лакунах).
Если последовательность натуральных чисел  , удовлетворяет условию
, удовлетворяет условию  , где
, где  , и ряд
, и ряд  имеет радиус сходимости
имеет радиус сходимости  , то все точки окружности
, то все точки окружности  являются особыми для функции
являются особыми для функции  .
.Возьмём теперь ряд

При

этот ряд мажорируется сходящимся рядом

, поэтому равномерно и абсолютно сходится в круге

. При
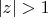
с помощью признака Даламбера легко проверить, что ряд

расходится. По теореме Адамара каждая точка окружности

является особой для суммы этого ряда, хотя ряд во всех точках окружности сходится.
В математической энциклопедии особая точка определяется как препятствие для аналитического продолжения элемента функции

вдоль какого-либо пути в комплексной плоскости.