Читаю книгу по применение теории представлений групп в квантовой механике, пытаясь понять, как они связаны между собой и с преобразованием Фурье.
Woit, Peter.
Quantum Theory, Groups and Representations. E-book, Springer, 2017.
Цитата:
Для представления

и элементов

группы

, близких к нейтральному элементу, можно записать

с помощью экспоненциальной функции как

где

тоже матрица, близкая к нулевой матрице. В дальнейшем мы изучим эту ситуацию намного более подробно на многих примерах и, в частности, покажем, что если

унитарен (то есть принадлежит подгруппе

), то

кососопряжённый:

где

— сопряжённо-транспонированная матрица. Положив

, находим, что

самосопряжённый

Теперь один из примеров, о которых сказано выше.
Цитата:
Если представление

на
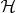
неприводимо, по теореме 2.2 оно одномерно с

. По теореме 2.3 оно должно иметь вид

для некоторого

. В этом случае самоспоряжённый оператор

— домножение элементов
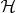
на целое

.
Тут я не понял. Кажется, надо задать самоспоряжённый оператор для
каждого элемента группы

.
Для справки,

.



