Можно, но не нужно. Мы разбиваем

не на произвольные вектора из

и

, а на конкретные, используя данное нам его разложение по

. Ну и обнаруживаем, что все коэффициенты в этом разложении были нулевые.
Все именно так, как вы пишете. Спасибо всем за обсуждение. Проверил все на примере для двух плоскостей. Действительно, если мы выбираем системы координат так, как написано в начале теоремы, то коэффициенты

должны обнулиться, иначе мы просто неправильно выбрали базисные вектора для

в начале процедуры и тогда вектор
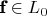
.
С другой стороны хочу обратить внимание участников обсуждения на другую интересную мысль, которая пришла во время обсуждения.
Для векторов подпространств будем писать вектор выделенным шрифтом, а в скобках указывать подпространство, к которому он принадлежит, например:

.
Тогда рассмотрим следующую последовательность шагов:
Шаг 1.

Шаг 2.
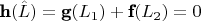
Шаг 3.

Шаг 4.

При этом, естественно,

и

.
Интересный вывод получился, нулевой вектор суммы подпространств
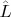
имеет ненулевые, но противоположные по знаку компоненты в суммируемых пространствах.
Пример:

, a

