В "линейной алгебре" застрял на теореме о сумме размерностей произвольных пространств. Посмотрел в трех учебниках:
Ильин, Позняк "Линейная алгебра" 2005 г, Теорема 2.9 стр 57
Канатников, Крищенко "Линейная алгебра", Теорема 2.5 стр 67
Мальцев "Основы линейной алгебры", теорема на стр 101.
Всюду однотипные доказательства и я никак не могу с ними согласиться. Мне кажется, что они неправильны. Попытался сформулировать свою точку зрения. Может кто-то сможет сказать, в чем у меня ошибка.
Теорема 2.9 (по Ильин, Позняк) о сумме размерностей произвольных подпространств.

Имеются два подпространства

и
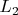
, пересечение этих подпространств обозначим

.
Чтобы построить базис подпространства

, строим последовательно базисы подпространств:
для

:

;
для

:

;
для

:
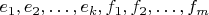
;
Чтобы доказать, что базисом для подпространства
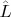
является набор векторов:

- надо доказать, что эти вектора линейно независимы. Для этого рассматривается линейная комбинация этих векторов, равная нулю:


(f.1)

Для сокращения дальнейших выкладок введем обозначения для векторов подпространства. Будем писать вектор выделенным шрифтом, а в скобках указывать подпространство, к которому он принадлежит, например:

.
Сокращенно формулу (f.1) можно записать так:

Далее в доказательстве говорится, что этот вектор разбивается на два, это понятно, т.к.

:
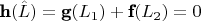
отсюда

Чтобы сумма двух векторов равнялась нулю, для слагаемых надо проверить два результата:
вариант1:
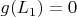
и

, т.е коэффициенты при всех векторах должны быть равны нулю;
вариант2:

и

, т.е. понять, каким образом вектора могут оказаться равными.
Доказательство теоремы сводится к получению варианта 1, но уже здесь в доказательстве произведена подмена. Если вектор принадлежит подпространству

, то для данного случая он должен выглядеть следующим образом:

т.е. разбиение линейной комбинации (f.1) произведено так, что у

коэффициенты при

равны нулю.
В доказательстве теоремы берется вектор

этот вектор находится в подпространстве

, и он не может быть разложен на компоненты в подпространстве

, как это сделано дальше в доказательстве теоремы.
Затем делается вывод, что коэффициенты разложения вектора
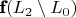
по
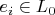
равны нулю. Подпространства не совпадают и разложение невозможно. Если, как и утверждается в теореме, это вектор, принадлежащий

, то его разложение дано в (f.2), т.е. вектор разложен по полному базису пространства

и другое разложение будет не верным. Поэтому разложение вектора
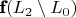
по базису подпространства

и вывод о равенстве коэффициентов

нулю выглядят, как ошибка.
Можно разбить вектор

по другому:

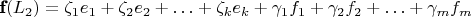
тогда коэффициенты при

точно не должны быть равны нулю.
Вариант2 в теореме не рассматривается. В этом варианте вектор
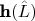
надо разбивать на сумму двух векторов из подпространства
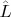
и доказывать их равенство.