Здравствуйте! Прошу помочь с двумя задачами по функциям нескольких переменных:
1. Найти
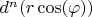 Моё решение:
Моё решение: Под знаком дифференциала функция двух независимых аргументов

. Тогда полный дифференциал n-го порядка запишется в виде

. Как мне кажется, слишком просто, чтобы это могло быть правильным решением. Но буду рад ошибаться

2. Оценить с помощью

погрешность приближения ф. Тейлора 1-го порядка для выражения
 Моя попытка решения:
Моя попытка решения: Выписал разложение

в окрестности точки

. Остаточным членом будет

. После вычисления частных производных и подстановки в остаток получается громоздкая дробь, где выбор величины
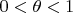
, на мой взгляд, совсем не очевиден
 Ход решения
Ход решения 




Благодарю за уделённое время




