Если не сложно, прокомментируйте мой третий вопрос
3. В данной ситуации следующие записи для выражения потенциала полностью тождественны?
Идём дальше.
В описанной мной ситуации, где есть только 2 заряженные пластины в вакууме, будем иметь следующее: это поле сформировано только свободными зарядами, так как мы условно считаем, что в проводнике, из которого сделаны пластины, есть только свободные заряды.
Отсюда получаем:

Если я правильно понимаю, в данном случае эти векторы в каждой точке пространства коллинеарны и сонаправлены, отличаются лишь длиной в

раз.
И вот дальше начинается самое непонятное.
Помещаем между обкладками конденсатор с диэлектрической проницаемостью

. В диэлектрике есть только связанные заряды. Фрагмент из учебника Савельева
 plenty of fish wilmington nc
plenty of fish wilmington ncОбозначим:

- напряжённость поля, создаваемого свободными и связанными зарядами пластин

- напряжённость поля, создаваемого свободными и связанными зарядами диэлектрика

- результирующая напряжённость поля

- индукция поля, создаваемого свободными зарядами пластин

- индукция поля, создаваемого свободными зарядами диэлектрика

- результирующая индукция поля
Имеем:

и соответственно


и соответственно

Поверхности пластин эквипотенциальны. Поверхности диэлектрика также эквипотенциальны.
Расстояние между платиной конденсатора и границей диэлектрика

Введём обозначения:

- потенциал левой пластины конденсатора (

)

- потенциал правой пластины конденсатора (

)

- потенциал левой границы диэлектрика (

)

- потенциал правой границы диэлектрика (

)
Ранее была формула потенциала любой точки пространства пространства, который создаётся зарядами конденсатора:

Найдём формулу для потенциала любой точки пространства, который создаётся зарядами диэлектрика:

Тогда результирующий потенциал любой точки пространства будет:

Найдём значений следующих потенциалов:




Найдём следующие разности потенциалов:




Просуммируем напряжения:

Далее построим график функции

при значениях

,

,

и

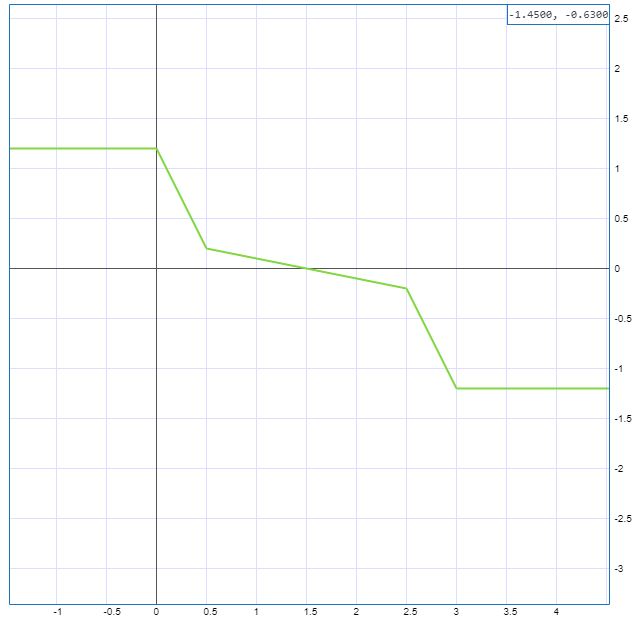
Вопросы:
1. Верны ли рассуждения?
2. Верен ли график (в том числе линейная зависимость потенциала от координаты внутри диэлектрика)?
3. Учитываются в задачах зазоры между пластинами конденсатора и диэлектриком и, если диэлектриков несколько, зазоры между диэлектриками?
4. В любых зазорах внутри конденсатора (зазоры между пластиной и диэлектриком, зазоры между разными диэлектриками) напряжённость поля равна той, что формируется только зарядами пластин конденсатора

?