4. Не очень понимаю разное количество аргументов в функции. Что это должно обозначать?
можно записать так

Первое равенство означает "потенциал является функцией от точки в пространстве (и больше не от чего)". Второе равенство означает, что точку в пространстве можно определить через декартовы координаты. Тогда "потенциал является функцией от декартовых координат точки в пространстве (и больше не от чего)". Это верно в общем случае в электростатике, но не в электродинамике!
Далее можем записать так:

.
Последнее равенство означает: так-то потенциал есть функция от всех трех пространственных координат (слева), но в рамках данной задачи он зависит только от координаты

(справа).
Остальные варианты я не понимаю.
Я как раз хотел узнать, как можно обозначить потенциал, если в рамках конкретной задачи он константа или если зависит только от одной переменной.
Вот это то, что я хотел узнать:
Потенциал константа:

Потенциал зависит от одной переменной:

.
Я задался эти вопросом, когда находил градиент, ибо там в там фигурируют частные производные для трёх переменных, а в задаче либо ноль, либо одна переменная.
Да, верен (для рассмотренного случая). Опять же - качественно верен, числа не проверял.
Значит, если мы оставим ту же формулу и введём между пластинами незаряженный проводник вместо диэлектрика, то за счет эквипотенциальности всего объёма проводника, график будет такой (график внутри проводника - прямая, параллельная оси х)?
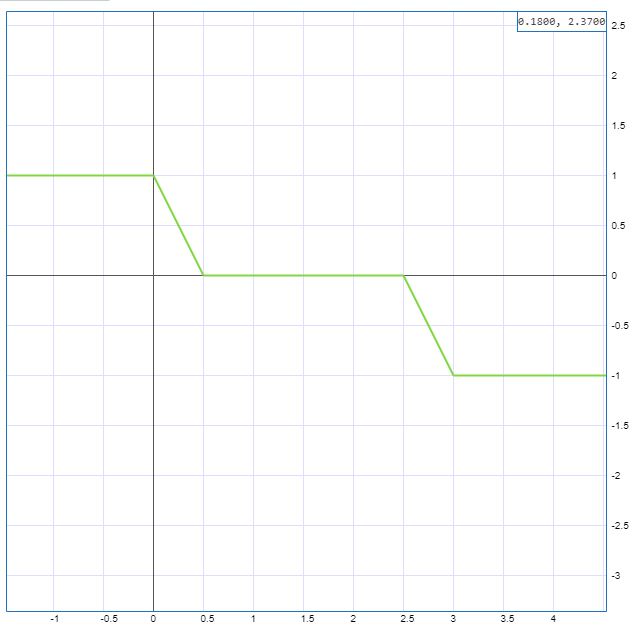
Получается, что введя незаряженных проводник в конденсатор мы как бы заменили этот конденсатор двумя последовательно соединёнными конденсаторами, так?
-- 14.05.2020, 19:31 --А что за ссылка прицепилась вместе с картинкой?
Видимо, сайт postimages.org иногда вставляет без моего ведома какие-то слова в ссылку.
-- 14.05.2020, 19:34 --Очень вам советую проникнуться этим вопросом сейчас. Там дальше (в обучении) у вас ещё, вероятно, появится векторный потенциал магнитного поля и на нём может случиться вывих мозга, лучше привыкайте к тому, что потенциал "определен с точностью до константы" сейчас, пока всё ясно и просто.
Уже проникся.