Задание: Доказать, что экспонента отображает алгебру косоэрмитовых матриц на группу унитарных, а алгебру кососимметричных матриц — на группу специальных ортогональных.
Для начала заметим, что экспонента сохраняет комплексное сопряжение и транспонирование, действительно:

Аналогично для комплексного сопряжения, тогда можем говорить, что

Пусть

- косоэрмитова матрица, тогда существует эрмитова матрица

, такая, что

, действительно,
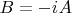
подходящая матрица , тогда пусть

, заметим, что

унитарно приводима к диагональному виду, причем на диагонали будут стоять действительные элементы, тогда:


Легко видеть, что

, в силу того, что
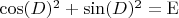
, значит

- унитарная матрица. Ну и легко показать, что для любой унитарной матрицы

, найдется косоэрмитова матрица

, т.ч.

. Действительно, т.к.

- унитарно приводима к диагональной матрице

и т.к. собственные значения

лежат на единичной комплексной окружности, то любой элемент диагонали матрицы

выражается как

, для некоторого

, тогда введем матрицу

, где

, тогда

, ну а тогда

, значит

- сюръективно отображает множество косоэрмитовых матриц на множество унитарных.

Теперь пусть

- кососимметричная матрица, тогда:

Значит

- ортогональная матрица, но более того
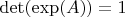
, действительно, т.к.

- кососимметричная матрица, то она подобна диагональной, причем элементы диагонали чисто мнимые и симметричны относительно нуля, тогда:

Значит,

- специальная ортогональная.
И дальше я не понял как доказать доказать, что


отображает множество кососимметричных матриц на множество специальных ортогональных ? Что тут можно сделать ?



