Известно следующие значения сдвига фаз:
1. Источник переменного питания:

2. Резистор:

3. Конденсатор:

4. Катушка индуктивности:

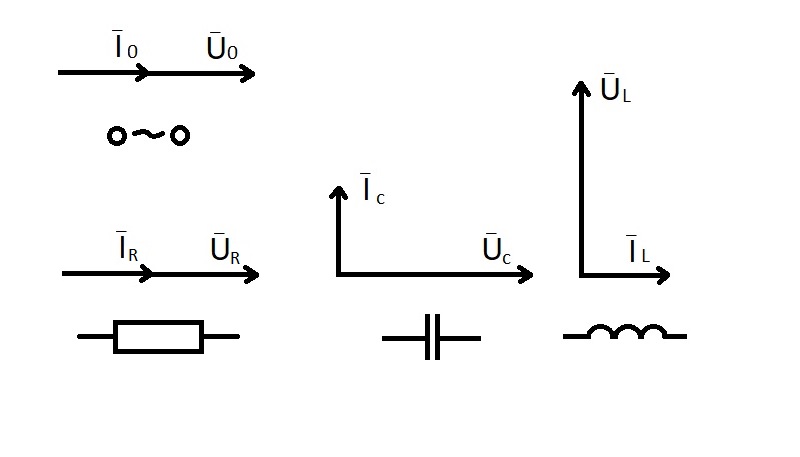
Соответствующие векторные диаграммы изображены на картинке.
Я не понимаю, как на физическом уровне происходит сдвиг фаз.
3 ситуации:
1я ситуация. Подсоединяем незаряженный конденсатор к источнику переменного питания, получается C-цепь.
Согласно второму закону коммутации

, т.е. напряжение на конденсаторе измениться скачком не может.
Пусть наш источник питания в момент времени

выдавал амплитудное значение напряжения

. На конденсаторе при этом в момент времени

напряжение

.
Получается, что для момента времени

не выполняется второй закон Кирхгофа. Для исправления ситуации добавим резистор последовательно с конденсатором, получаем RC-цепь. Теперь в момент времени

на резисторе напряжение

и второй закон Кирхгофа выполняется.
Получается, что в момент времени

напряжение источника и напряжение резистора опережают по фазе напряжение на конденсаторе:

.
Вопрос: что с током в цепи в момент времени

?
Я предполагаю, что ток есть и он максимален

Отсюда получается, что уже в момент времени

на конденсаторе МГНОВЕННО формируется разность фаз между током и напряжением.
Ниже представлена векторная диаграмма RC-цепи.
 free picture upload sites
free picture upload sites2я ситуация. Подсоединяем катушку индуктивности к источнику переменного питания, получается L-цепь.
Согласно первому закону коммутации

, т.е. ток на катушке измениться скачком не может.
Пусть наш источник питания в момент времени

выдавал амплитудное значение напряжения

. На катушке при этом в момент времени

напряжение

.
Получается, что для момента времени

выполняется второй закон Кирхгофа.
Смотрим ток. В момент времени

ток источника максимален

(в противном случае не будет соблюдаться векторная диаграмма для источника питания), ток катушки отсутствует

и первый закон Кирхгофа нарушается.
Для исправления ситуации добавим резистор параллельно с катушкой, получаем RL-цепь. Теперь в момент времени

на резисторе напряжение

и ток

, при этом первый закон Кирхгофа выполняется.
Получается, что в момент времени

ток источника и ток резистора опережают ток катушки:

.
Получается, что уже в момент времени

на катушке МГНОВЕННО формируется разность фаз между током и напряжением.
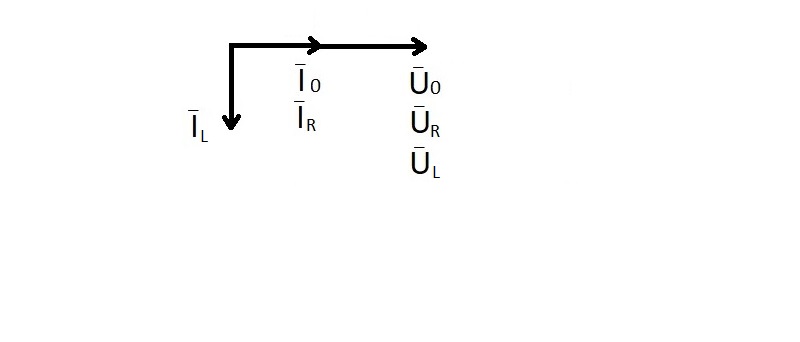
Ниже представлена векторная диаграмма RL-цепи.
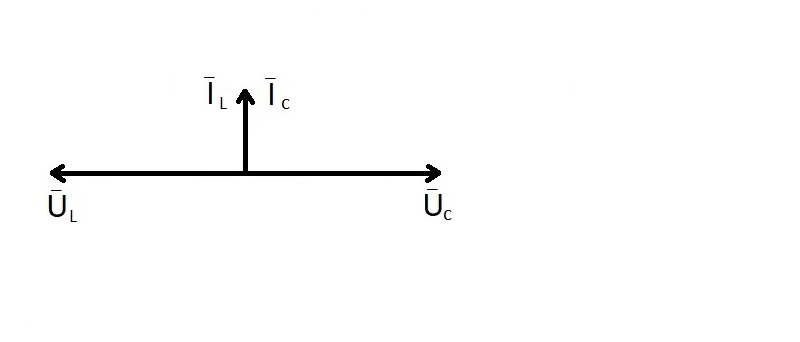
3я ситуация - LC-цепь (колебательный контур).
Ниже представлена векторная диаграмма LС-цепи.
Вопросы:
1. Верны ли рассуждения?
2. Верны ли векторные диаграммы?



