Здравствуйте. Возникло два маленьких момента по теории поля, первый - по скалярному, второй - по векторному.
1) Вопрос по терминологии. Рассмотрим скалярное поле

, заданное в трёхмерном пространстве. Говорится, что точки

для которых поле принимает некоторое постоянное значение

,
вообще говоря, заполняют некоторую поверхность (или несколько раздельных поверхностей), которые называются поверхностями уровня. Но ведь,
вообще говоря, эти точки могут заполнять некоторый объем (или несколько раздельных объемов) пространства. Значит слово "поверхности" в термине "поверхности уровня" чисто условное? То же самое можно привести по отношению к линиям уровня скалярного поля, заданного на плоскости. Там ведь тоже точки могут заполнять площадь (плоскую область),
вообще говоря. Кстати, если в трёхмерном пространстве точки заполняют линию, то как её назвать? Линией уровня или поверхностью уровня?
2) Говорится, что можно характеризовать величину вектора векторного поля густотой проводимых линий. Для этого через каждую точку проводим маленькую ортогональную к линии площадку, считаем количество пересечений её с векторными линиями и делим на площадь площадки. Я не вижу, как эта характеристика может характеризовать величину вектора векторного поля. Или это справедливо только для определенного "типа" векторных полей? Например, зная закон Кулона и рассматривая электрическое поле вокруг неподвижного заряда, я понимаю что густота линий будет ближе к заряду и там действительно напряженность поля больше. Но будет ли там пропорциональность или другая зависимость (одинаковая для каждой точки) этой напряженности и количества пересекаемых линий единичной площадкой? А вот для придуманного мною поля
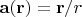
во всех точках (кроме начала координат) векторы будут единичными. Густота векторных линий здесь тоже увеличивается к началу координат, но это не може характеризовать величину векторов поля, поскольку они все имеют единичную длину. Как тут быть?
-- 02 май 2020, 12:15 --UPD: Рассмотрим ещё поля

и

. В данной точке густота векторных линий обеих полей одинакова, но величины векторов в данной точки разные. Значит зависимости между величиной вектора и количеством пересекаемых линий будут разные. А можно ещё написать поле

. Здесь зависимость будет ещё другой. Интересно, будут ли эти зависимости зависеть от точки?
-- 02 май 2020, 12:18 --UPD2: Хотя, если для поля
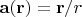
такая зависимость имеет место быть, значит она должна зависеть от точки.



