допустимо ли такое преобразование

[kotenok gav]

SPgum в сообщении #1458685 писал(а):

Не подскажите в каком разделе можно поискать?!

Подскажу: в гугле.

[Утундрий]

(Оффтоп)

SPgum в сообщении #1458685 писал(а):

не нашол! Не подскажите

глоза краваточет сатреть

[SPgum]

Большое спасибо за разъяснения! В разделе "Сравнение бесконечно малых величин" я нашел ответ!
Тогда, если я правильно понял, нельзя использовать определение для эквивалентности бесконечно малых величин одного порядка в отношении $\frac{dx}{dx}$, поскольку их отношение не имеет предела $\lim\limits_{x\to 0} \frac{dx}{dx}=\frac{0}{0}$ ?

[kotenok gav]

$\dfrac{dx}{dx}=1$ по определению производной.

[SPgum]

Спасибо за ответ, но прошу прощения, что то я запутался: Ведь по определению это отношение приращения функции к приращению переменной, а при эквивалентности речь шла о бесконечно малых величинах: А.Ф. Бермант, И.Г. Араманович "Краткий курс математического анализа". Т.е. я сделал не верный вывод относительно $\lim\limits_{x\to 0} \frac{dx}{dx}=\frac{0}{0}$

[kotenok gav]

Бесконечно малые приращения обозначаются $\Delta x$. $\lim\limits_{\Delta x\to0}\dfrac{\Delta x}{\Delta x}=1$.

[arseniiv]

SPgum в сообщении #1458835 писал(а):

Т.е. я сделал не верный вывод относительно $\lim\limits_{x\to 0} \frac{dx}{dx}=\frac{0}{0}$

Если у вас $dx$ это какие-то отдельные штуки (например дифференциалы), то они не зависят никак от $x$ и предел по $x$ от них брать смысла нет, а ответ будет равен 1. Если это цельное обозначение производной, то опять же предел брать нет смысла, потому что она мало того что непрерывна в нуле (и можно было бы не брать предел, а подставлять сразу ноль), она вообще тождественно равна 1. Наконец вы ещё могли иметь в виду $\lim\limits_{x\to 0} \frac xx$, но и он разумеется будет равен единице. Или вы имели в виду ещё что-то, но не понятно что.

Если это как-то должно быть связано с бесконечно малыми величинами (сразу оговорим базу $x\to0$), то $dx$ это не бесконечно малая величина (это функция двух аргументов), а вот $x$ или $\sin x$ — да.

[SPgum]

Большое спасибо за объяснение (когда учился в вузе, было как то не актуально, а вот теперь понадобилось). Если Вас не затруднит, не могли бы Вы пояснить физический смысл величины $ {dx}$ в записи для интеграла

$$ \int_{0}^{x}{f(x)}{dx}$$

В учебнике сказано, что $ {f(x)}{dx}$ - это подынтегральное выражение,
$ {x}$ - переменная интегрирования,
Но, что тогда представляет собой в этом выражении запись $ {dx}$, каков его физический смысл и можно ли воспринимать $ {f(x)}{dx}$ как произведение $ {f(x)}$$ и $ {dx}$$?
Почему нельзя сокращать на $ {dx}$ в числителе и знаменателе произведения

$$\frac{dw(x)}{dx} \int_{0}^{x}{dx}\neq\int_{0}^{x}{dw(x)}={w(x)}$$

Буду очень признателен !

[kotenok gav]

SPgum в сообщении #1458915 писал(а):

физический смысл величины $ {dx}$

Примерно то же самое, что и для производной: значение в точке умножаем на приращение аргумента.

[SPgum]

kotenok gav в сообщении #1458917 писал(а):

SPgum в сообщении #1458915 писал(а):

физический смысл величины $ {dx}$

Примерно то же самое, что и для производной: значение в точке умножаем на приращение аргумента.

Спасибо за ответ, но честно говоря, вопрос не сильно прояснился после фразы " примерно" и в учебниках не нашел разъяснения

[arseniiv]

SPgum в сообщении #1458915 писал(а):

Но, что тогда представляет собой в этом выражении запись $ {dx}$, каков его физический смысл и можно ли воспринимать $ {f(x)}{dx}$ как произведение $ {f(x)}[math]$$ и $ {dx}$$?

С одной стороны это $dx$ можно воспринимать просто как указание переменной, по которой мы интегрируем. С другой стороны всё подынтегральное выражение здесь можно понимать как 1-форму, но интегрирование 1-форм придётся определять и изучать отдельно. Хотя оно и довольно красиво, но прям с нуля я не возьмусь объяснять так, чтобы гарантированно не запутать.

Ну а «физически» $dx$ это действительно такая длина пренебрежимо малого отрезочка, $f(x)\,dx$ — площадь тоненькой криволинейной трапецийки между графиком функции и $x=0$, и интеграл это как бы сумма всех таких площадей для разбиения области интегрирования на такие пренебрежимо малые отрезки.

SPgum в сообщении #1458915 писал(а):

Почему нельзя сокращать на $ {dx}$ в числителе и знаменателе произведения

$$\frac{dw(x)}{dx} \int_{0}^{x}{dx}\neq\int_{0}^{x}{dw(x)}={w(x)}$$

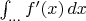
Потому что грубо говоря одно под интегралом, а другое не под. Вот если бы было $\int_{\ldots} f'(x)\,dx$, мы бы получили теорему Ньютона—Лейбница, в которой как раз «сокращается».

-- Ср апр 29, 2020 21:18:55 --

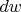
То есть на таком рукомахательном уровне ошибка выше в заносе $dw(x)$ в интеграл. Вне интеграла это выражение от одного какого-то значения икса, а под интегралом мы перебираем все иксы, совсем другой смысл и потому туда-сюда таскать выражения, зависящие от переменной интегрирования, нельзя. (А если попытаться сократить без заноса $dw$, получится очевидно бессмысленная запись.)

[SPgum]

Большое спасибо!!! По крайне мере для меня, что то стало более обоснованным! Еще раз Большое спасибо!

-- 29.04.2020, 19:33 --

arseniiv в сообщении #1458934 писал(а):

Вне интеграла это выражение от одного какого-то значения икса, а под интегралом мы перебираем все иксы

Покрайне мере в этой части,для меня картина прояснилась!!!

[Someone]

SPgum в сообщении #1458835 писал(а):

по определению это отношение приращения функции к приращению переменной

Неверно. Производная — это не "отношение приращения функции к приращению переменной".

SPgum в сообщении #1458775 писал(а):

их отношение не имеет предела $\lim\limits_{x\to 0} \frac{dx}{dx}=\frac{0}{0}$ ?

Поскольку $\frac{dx}{dx}=1$ независимо ни от какого $x$ (и вообще $dx=\Delta x$ есть приращение независимой переменной $x$, которое никаким боком от $x$ не зависит), то указанный предел есть просто $\lim\limits_{x\to 0}1=1$.

kotenok gav в сообщении #1458842 писал(а):

Бесконечно малые приращения обозначаются $\Delta x$.

С какой стати приращения стали бесконечно малыми? Да и дифференциалы нисколько не бесконечно малые.

SPgum в сообщении #1458915 писал(а):

$$ \int_{0}^{x}{f(x)}{dx}$$

Очень плохое обозначение. Крайне желательно, чтобы обозначение переменной интегрирования отличалось от обозначения предела интегрирования и вообще нигде, кроме подынтегрального выражения не встречалось. Например, можно было бы написать

$$\int_0^xf(\tau)d\tau;$$

тогда у Вас не было бы искушения сокращать $d\tau$ внутри интеграла с $dx$ снаружи.

SPgum в сообщении #1458915 писал(а):

Но, что тогда представляет собой в этом выражении запись $ {dx}$

Здесь $dx$ — часть обозначения интеграла. Воспринимайте значки $\int$ и $dx$ в записи интеграла как своего рода скобки, между которыми стоит подынтегральная функция; отрывать одну скобку от другой и сокращать её с чем-нибудь нельзя. Надеюсь, Вы не сокращаете правые скобки в числителе и знаменателе дроби?

[SPgum]

Someone в сообщении #1459010 писал(а):

Например, можно было бы написать

$$\int_0^xf(\tau)d\tau;$$

тогда у Вас не было бы искушения сокращать $d\tau$ внутри интеграла с $dx$ снаружи.
Но, что тогда представляет собой в этом выражении запись $ {dx}$ Здесь $dx$ — часть обозначения интеграла. Воспринимайте значки $\int$ и $dx$ в записи интеграла как своего рода скобки, между которыми стоит подынтегральная функция; отрывать одну скобку от другой и сокращать её с чем-нибудь нельзя.

Большое Спасибо за разъяснение!!! Если воспринимать как скобки, тогда бесспорно! Очень доходчиво!!!

Еще раз, всем Большое Спасибо за помощь!!!