Вектор состояния квантового поля

[vlad9486]

В нерелятивистской квантовой механике с фиксированным количеством частиц вектор состояния (волновая функция) - это функция времени и $3n$ переменных, где $n$ - количество частиц, а значения у нее - комплексные числа. А с квантовым полем сложнее. Насколько я понял, это функция, которая определена на полевых конфигурациях, то есть область определения у нее - полевые функции. Используя обозначения теории типов, тип состояния (например) электронного поля:

$(\mathbb{R} ^ 4 \to SU(2) \times SU(2)) \to \mathbb{C}$

Функция принимающая (функцию принимающую точку пространства времени и возвращающую биспинор) возвращающая комплексное число. Непонятно почему в конце комплексное число, может быть это сразу квадратный корень вероятности:

$(\mathbb{R} ^ 4 \to SU(2) \times SU(2)) \to \mathbb{R} ^ +$

Это реально непонятный момент, а в учебнике за обозначениями таких деталей не видно. Вообще плохо освещено состояние квантового поля.

[Alex-Yu]

vlad9486 в сообщении #1457897 писал(а):

может быть это сразу квадратный корень вероятности:

Квантовая физика (хоть частиц, хоть поля) в терминах вероятности не описывается. Вместо вероятностей нужны комплексные амплитуды. Почему-то в случае механики фиксированного числа частиц у вас комплексная амплитуда возражений не вызывает. А как поле -- так сразу какие-то странные затеи. Хотя в этой части все совершенно одинаково.

-- Вс апр 26, 2020 01:58:45 --

vlad9486 в сообщении #1457897 писал(а):

А с квантовым полем сложнее.

Да не сказать, что так уж сложнее (на идейном уровне). Каждой конфигурации сопоставляется (комплексная) квантовая амплитуда. Конфигурация $n$ частиц -- это $3n$ чисел (координат). Конфигурация поля -- это полевая функция. Все то же самое, только в полевом случае динамических координат бесконечно много (каждое значение полевой функции, нумеруемое пространственными координатами -- это независимая динамическая координата; т.е. пространственные координаты в полевом случае играют роль "индексов" различающих динамические полевые координаты).

[arseniiv]

vlad9486 в сообщении #1457897 писал(а):

и возвращающую биспинор

Они разве в $\mathrm{SU}(2)\times\mathrm{SU}(2)$ живут?

[physicsworks]

vlad9486 в сообщении #1457897 писал(а):

Насколько я понял, это функция, которая определена на полевых конфигурациях, то есть область определения у нее - полевые функции.

В шредингеровской картине это функционал над (комплекснозначным) полем. В гейзенберговской картине --- это операторозначное распределение (это распределение нужно "размазать" квадратично интегрируемыми функциями чтобы получить хорошо определенные операторы). Операторы (рождения и уничтожения частиц) при этом действуют на состояния Фока (которые строятся по неприводимым представлениям группы Пуанкаре). В КТП практически всегда используется более удобная гейзейнберговская картина, в которой динамика переносится на гейзенберовские поля-операторы (на самом деле распределения, как я написал выше), из которых строятся Лоренц-ковариантные корреляционные функции Грина, из которых посредством LSZ-формализма получаются матричные элементы $S$-матрицы. Удобность гейзенберовской картины в том, что ультрафиолетовые расходимости в функциях Грина удобно изолировать и ренормализировать в Лоренц-ковариантном виде (при этом, как только мы эту процедуру осуществим для функций Грина, мы автоматически получаем элементы $S$-матрицы, свободные от ультрафиолетовых расходимостей). В фейнмановоском подходе к КТП, который более удобен для недетских теорий, комплексная амплитуда перехода вакуум-вакуум (состояния здесь опять же в гейзенберовской картине, у них есть ярлычки соответствующие временам, но сами состояния от времени не зависят; конкретно здесь эти ярлычки есть $-\infty$ и $+\infty$) есть интеграл по классическим полевым конфигурациям (от комплексной экспоненты с классическим действием как функционалом от классического поля: $\exp(iS[\text{field}]$), и можно сразу построить производящий функционал $Z[J]$, "включив" классический источник $J$. Фундаментальные корреляционные функции Грина (из которых получаются элементы $S$-матрицы посредством LSZ) даются простым функциональным дифференцированиям $Z[J]$ по источникам $J$ с последующим обнулением источников. Функции Грина посчитать точно можно только в исключительных случаях и обычно их находят пертурбативно.

vlad9486 в сообщении #1457897 писал(а):

В нерелятивистской квантовой механике с фиксированным количеством частиц вектор состояния (волновая функция) - это функция

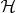
вектор состояния и волновая функция --- это разные вещи. Если у меня есть вектор состояния $|state \rangle$, живущий в неком гильбертовом пространстве $\mathcal{H}$, то волновая функция (например, для простоты в координатном представлении) есть $\psi(x) \equiv \langle x | state\rangle$.

vlad9486 в сообщении #1457897 писал(а):

Это реально непонятный момент, а в учебнике за обозначениями таких деталей не видно. Вообще плохо освещено состояние квантового поля.

в учебниках все это есть. Например, в Вайнберге.

[vlad9486]

arseniiv в сообщении #1457925 писал(а):

vlad9486 в сообщении #1457897 писал(а):

и возвращающую биспинор

Они разве в $\mathrm{SU}(2)\times\mathrm{SU}(2)$ живут?

Ошибка. Там должно быть $\mathbb{C} ^ 2 \times \mathbb{C} ^ 2$, а $\mathrm{SU}(2)\times\mathrm{SU}(2)$ это тип оператора, который на них действует.

Вот поэтому и вопрос возник, вроде комплексные числа уже есть и странно что они два раза в типе функции встречаются.

-- 26.04.2020, 08:59 --

physicsworks в сообщении #1457977 писал(а):

В шредингеровской картине это функционал над (комплекснозначным) полем.

Классическое поле принимает точку и возвращает комплексное число, а квантовое поле принимает классическое поле и возвращает комплексное число (потому его называют не функция, а функционал, но в терминологии теории типов это все функции). И это меня удивляет, потому что комплексное число возникает два раза.

Боюсь что без понимания этого всего (и особенно гейзенберговской картины) я не смогу вот так сходу перевести все на язык теории типов.

[physicsworks]

vlad9486, вам выше Alex-Yu объяснил этот момент. Прочитайте последний параграф внимательно.

[Alex-Yu]

vlad9486 в сообщении #1457991 писал(а):

И это меня удивляет, потому что комплексное число возникает два раза.

Подозреваю, что корень непонимания заключается в следующем. Пространственные координаты играют совершенно разную роль в механике частиц и теории поля (причем уже для классических полей и частиц, квантовость тут ни при чем). В механике частиц пространственные координаты есть динамические переменные. Они задают положение частицы, это не просто координаты вообще, это координаты частицы. В теории поля ситуация совсем другая (причем уже в классической теории): здесь пространственные координаты это ни в коем случае не динамические переменные, это просто континуальные индексы, "ярлыки", отличающие одну динамическую переменную от другой. В теории поля динамическими переменными (обобщенными координатами в смысле лагранжевой механики) являются значения поля (полевой функции) в разных пространственных точках.

Ну а на счет "два раза комплексное число"... Ну это вообще ни о чем. Возьмите для начала действительное скалярное поле, и никакой двухкратной комплексности не будет. Полевая функция будет просто действительным скаляром. Поля разные бывают, на дираковском биспинорном поле свет клином не сошелся. Все это идет от совершенно дурацкого, применительно к КТП, термина "волновая функция"!!! Не надо путать две совершенно разные вещи: полевую функцию и "волновую функцию", которую правильней вообще так не называть (это вектор состояния, если хотите комплексный функционал, но никак не функция пространственных координат). "Волновая функция" -- это из механики частиц, к полям она вообще никакого отношения не имеет (хотя исторически так сложилось, что так, крайне неудачно, иной раз говорят и в КТП).

[vlad9486]

Аргументом функции состояния в механике частиц выступают координаты, а результатом амплитуда вероятности. В теории поля аргументом выступает поле (которое и само есть функция), а результатом опять амплитуда вероятности.

Я понимаю что (как toy model) можно рассмотреть действительное скалярное поле, но реально все фундаментальные фермионные поля комплексные (да еще и биспиноры). Но это комплексное число - не амплитуда вероятности (или я не прав и ее тоже можно как-то так интерпретировать?). Вот это вот интересно, случайно ли что и итоговая амплитуда вероятности и полевая функция комплексные?

С самого начала я даже сомневался что там у нас в конце башни функций $\mathbb{C} или $\mathbb{R}^+, потому что появление комплексных чисел два раза казалось странностью. Но насколько я понял, в картине Шредингера комплексное скалярное поле будет функционалом такого типа: $(\mathbb{R}^4\to\mathbb{C})\to\mathbb{C}$.

[Утундрий]

vlad9486
Ну вот вы согласны рассматривать только комплекснозначные поля:

vlad9486 в сообщении #1458272 писал(а):

реально все фундаментальные фермионные поля комплексные (да еще и биспиноры)

А потом у вас удивление:

vlad9486 в сообщении #1458272 писал(а):

Вот это вот интересно, случайно ли что и итоговая амплитуда вероятности и полевая функция комплексные?

Как вы оцените нетривиальность этого "совпадения"?

[arseniiv]

Вполне резонный вопрос, что такое значения поля (не квантового, а того, на которых квантовое поле функционал), являющиеся комплексными числами. Вон в классической электродинамике значения поля — антисимметричные тензоры второго ранга, но хотя бы вещественные, и им довольно просто придать геометрический смысл, а тут бац комплексные. Если бы я был ТС, я бы непременно спросил.

[Xaositect]

Ну вообще комплексность спиноров - это вопрос чисто обозначений, ибо умножать их на комплексные числа, вообще говоря, никому не нужно. Их нужно умножать на элементы $\mathrm{Spin}(3, 1)$, а то, что эта группа оказалась изоморфной $\mathrm{SL}(2)$ - это вещь случайная.

[Alex-Yu]

vlad9486 в сообщении #1458272 писал(а):

Но это комплексное число - не амплитуда вероятности (или я не прав и ее тоже можно как-то так интерпретировать?). Вот это вот интересно, случайно ли что и итоговая амплитуда вероятности и полевая функция комплексные?

Случайно. Никакого глубокого смысла здесь нет. И вообще комплексное число -- это пара действительных, и ничего более. Смысл надо искать не в разновидности чисел, а в лагранжиане. Некоторые лагранжианы удобнее (но вовсе не обязательно) записывать через комплексные поля. Но можно, в принципе, и через действительные, удвоив число полей. Например говорят, что заряженные поля описываются комплексными полями. Отнюдь не обязательно. Калибровочная группа электродинамики -- это $U(1)$, но она изоморфна $SO(2)$ и можно построить электродинамику на основе $SO(2)$. Правда, получится не очень естественно: исходными полями будут суперпозиции электрона и позитрона. Вершина будет не диагональна: будет переводить одну суперпозицию электрона и позитрона переводить в другую суперпозицию. Зато все поля будут действительными. Но к обычным полям (уже комплексным) с обычной диагональной вершиной можно будет перейти банальным унитарным преобразованием.


В общем позабавляться этим можно, но никакого содержательного результата это не даст. Ибо ничего содержательного здесь просто нет.

[Утундрий]

Кстати, Майорана как-то извратился и записал уравнение Дирака без единой мнимой единицы

[Alex-Yu]

vlad9486 в сообщении #1458272 писал(а):

все фундаментальные фермионные поля комплексные (да еще и биспиноры). Но это комплексное число - не амплитуда вероятности

Естественно. Полевая функция никакого отношения к амплитуде вероятности не имеет. Ни малейшего отношения!!!

-- Пн апр 27, 2020 22:35:05 --

vlad9486 в сообщении #1458272 писал(а):

комплексное скалярное поле будет функционалом такого типа: $(\mathbb{R}^4\to\mathbb{C})\to\mathbb{C}$.

Все же не поле этим будет, а вектор состояния поля. Поле же после квантования станет операторнозначной на векторах состояния функцией от $\mathbb{R}^4$.

[physicsworks]

Alex-Yu в сообщении #1458290 писал(а):

Смысл надо искать не в разновидности чисел, а в лагранжиане.

+1 Вообще, ТС ищет сакральный смысл там, где его нет. Это мне напоминает когда математики (не матфизики, а чистые математики) пытаются разобраться в квантах или, еще хуже, в КТП. Ну, на долго их все равно не хватает... (и хорошо)