Задана

функция

,

для всех

. Пусть

задана как

Соответственно,

- симметричная и положительно полуопределенная. Пусть

это минимальное собственное число матрицы

,

. На сколько я понимаю, функция

будет непрерывной, неубывающей, но не обязательно везде дифференцируемой. Однако, для неё справедливо

для всех

и
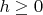
и некоторого

.
Вопрос - справедливо ли неравенство выше и как связать

и C?
-- 16.04.2020, 18:49 --Подумал, что

Каждый элемент матрицы

меньше, чем

, а отсюда можно выйти на ограничения свержу для максимаьного собственного числа, и, соответственно,

. Верно?



