Тякс, пока был сегодня за двором днем, порисовал немного в тетради и подумал, а теперь, перерисовал это все на компьютере когда в хату. Получилось следующее что задача имеет жестки ограничения, например:
— расчет по последнему прибывшему на базу это обязательное граничное условие встречи всех троих в одно время на одном расстоянии от старта что равняется расстоянию до базы;
— вот это "Велосипедист довозит второго туриста до некоторой точки дороги, откуда тот продолжает движение пешком, и возвращается за третьим.", означает что обазятельно будет точка где все три встретятся, и обязательно велосипедист одного заберет, то есть велосипед
не может высадить пассажира где попало, это существенно думаю тоже.
Итак, держа в голове эти условия у нас сразу вырисовывается интересная картинка, диаграмма

, какие полезные диаграммы однако! Вышеупомянутая диаграмма этого, эдакого движения будет состоять из циклов, каждый цикл это пять стрелочек: встреча всех троих в одном месте в одно время, далее велосипедист повез одного а второй потопал пешком, дальше велосипед высаживает где нибудь пассажира и едет за вторым, подбирает его —
а затем едет в место встречи всех троих со своим пассажиром, и цикл повторяется. Это на рисуночке будет параллелограммик с центральной меньшей диагональю в виде стрелочки.
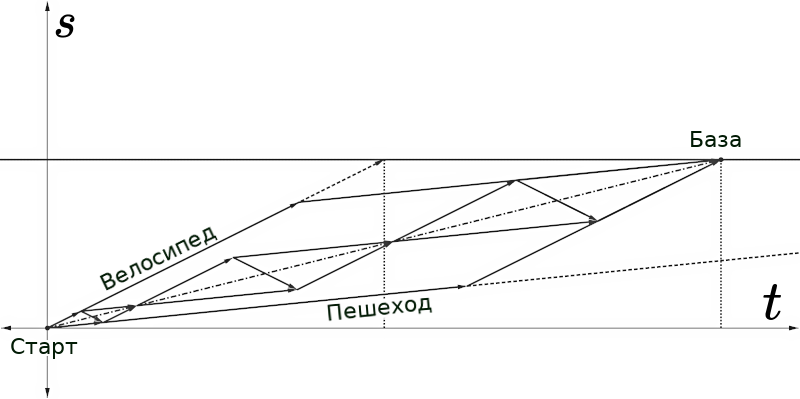
Допустим сначала я беру три таких произвольных цикла (вспоминаем граничное условие номер один), и довожу ими всех до базы. Потом беру один цикл (а почему бы и нет), и мы видем что длинные диагонали всех троих маленьких и одного большого параллелограмма есть
параллельные. То есть средние скорости будут одинаковы при любом количестве (кроме бесконечного, которое количеством назвать нельзя) циклов! А все потому что угол между стрелочками будет зависеть только от скоростей, ну то есть скорость определяет тангенс угла, в результате все параллелограммы подобны, более того, и стороны параллельны так как движение непрерывное и один идет сразу за другим. И диагонали у всех будут параллельны, соответственно будут один единственный наклон относительно оси времени

, поэтому единственно возможная, и оно же максимальная средняя скорость будет наклон большей диагонали любого из параллелограммов.
Но как же посчитать этот наклон имея при себе только наклоны двух сторон параллелограмма? Ответ очевиден — повернуть систему нашу систему координат так чтобы ось времени совпала с пешеходом, то есть перейти в систему отсчета пешехода! Абсолютно гениально! О таком переходе мне вроде кстати говорили
waxtep вроде с самого начала. Итак вспоминая все граничные условия и рисунок выше...
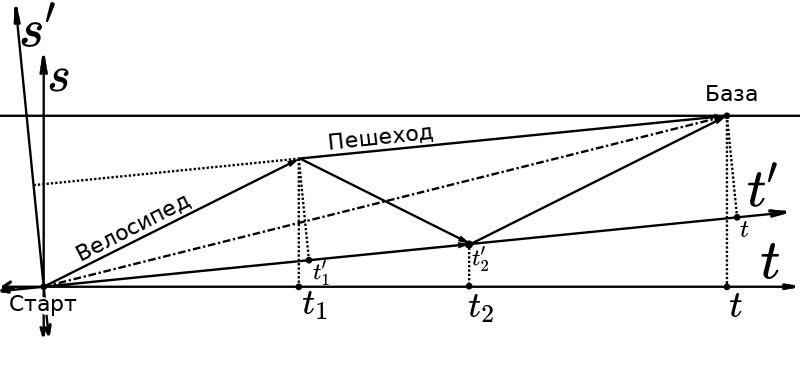
Пусть момент времени

это момент встречи всех троих на базе после одного цикла, зачем нам усложнять если много циклов дадут тот же самый уклон, оно же средняя скорость,

— это момент времени когда велосипед высадил первого пассажира и поехал за вторым, при этом он отдалился от места старта на некоторое расстояние

, надо было пометить на рисунке, ну нехай, как говорил один старый преподаватель практики по физике — к лешему! Система отсчета что связана со вторым пешеходом пока он не был подобран велосипедом это

, также вспоминаем что для любого момента времени

для системы отсчета связанной например с базой —

, слава богам не теория относительности!

Сразу видим что расстояние

от нуля будет такое же как расстояние до базы в момент встречи всех троих в штрихованной системе. То есть начинаем понимать почему оно сократится! Запишем первый момент времени

естественно скорость велосипеда в системе отсчета пешехода будет меньше нежели в системе отсчета базы, и сразу же, не отходя от кассы, запишем и второй момент времени

и таки да, третий момент времени будет найден аналогичным образом

то есть на паралеллограмик на самом деле ромбик! Не смотря на то что у меня нарисовано, правильно печатали
Утундрий, и не правильно в тоже время, в том смысле что я не игнорирую замечания, просто иногда недопонимаю... Действительно, в ромбике дело! Запишем же наконец среднюю скорость по формуле какую я почему-то не взял во внимание но мне напомнили
slavav
А теперь попробуем как-то перевести эту скорость в систему отсчета базы, просто додадим к этой скорости, скорость пешехода

Хух! Примерно понятно! И месяца не прошло...

Капец у меня темпы.
wrestГде у меня что конкретно неправильно посчитано в последних сообщениях с расчетами на предыдущей странице? Там все моменты времени и все величины озвучены. Почему эта скорость больше чем та, при которой сперва довозит велосипедист до базы одного а потом возвращается за вторым?
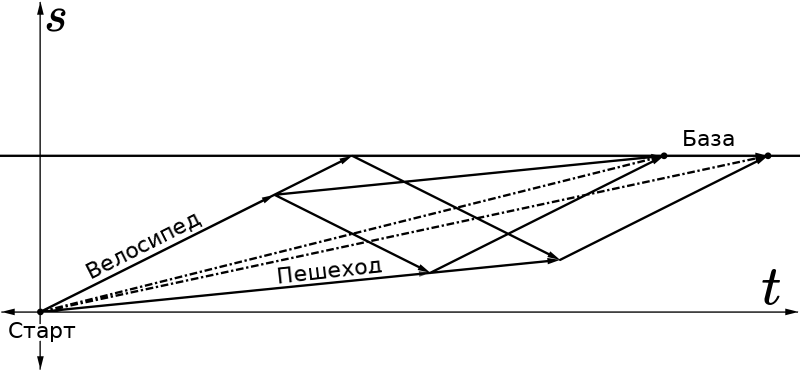
Потому что во случае подвоза прямо на базу велосипед отдалится дальше (на максимально возможное с соблюдением граничных условий) расстояние от второго пешехода, а при подвозе в точку откуда если высадить пешехода он уже потопает на базу без помощи, велосипед будет ехать прямиком на базу пока в первом случае он бы ехал только за вторым.
AmwТам

примерно с рисунка, а не десять.