О производной неявной функции

[Evgenii2012]

Дорогие друзья ! Позвольте мне проконсультироваться с Вами по поводу относительно простой задачи из книги Н.А. Давыдов, П.П. Коровкин, В.Н. Никольский. Сборник задач по математическому анализу. - М.: Просвещение, 1964. Это задача 1932 на стр. 121 в этой книге. Итак, требовалось найти
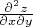
$\frac{\partial^2 z}{\partial x\partial y}$ для функции, заданной неявно соотношением

$$x^2+y^3+z^4=x+z.\qquad(1)$$

Проблема в том, что у меня решение не сходится с ответом в книге, поэтому хотелось бы узнать Ваше мнение: эту задачу я неправильно решаю, или -- ошибка в книге ? Привожу ниже решение задачи, вот оно. Дифференцируя (1) по $x$ получим:

$$2x+4z^3\cdot z_x=1+z_x\,,\qquad(2)$$

где, как обычно, $z_x:=\frac{\partial z}{\partial x}.$ Теперь дифференцируем (2) по $y,$ получаем:

$$12z^2\cdot z_xz_y+4z^3\cdot z_{xy}=z_{xy}\,.\qquad(3)$$

Выносим в (3) за скобки $z_{xy},$ получаем:

$$z_{xy}(1-4z^3)=12z^2z_xz_y\,.\qquad(4)$$

Из соотношения~(2) $z_x(1-4z^3)=2x-1,$ $z_x=\frac{2x-1}{1-4z^3}.$ Из
(1) также имеем (дифференцированием по $y$), что

$$3y^2+4z^3\cdot z_y=z_y\,,$$

$$3y^2=z_y(1-4z^3)\,.$$

Тогда из (4) получаем ответ, что

$$z_{xy}=\frac{12z^2z_xz_y}{(1-4z^3)}=\frac{36z^2(2x-1)y^2}{(1-4z^3)^3}\,.$$

В то же время правильный ответ из книги:

$$\frac{36(1-2x)z^2y^2-2(4z^3-1)^2}{(4z^3-1)^3}\,.$$

Вопрос: всё ли правильно я делаю ? Такой вопрос у меня возник ещё и в связи с тем, что решая предыдущую задачу 1931 (найти $\frac{\partial^2z}{\partial x^2}$ для функции, заданной неявной соотношением $x^2+y^2+z^2=2z$) у меня также не сошлось с ответом. У меня получается ответ $z_{xx}=\frac{1-2z+z^2+x^2}{(1-z)^3},$ а в книге ответ
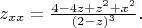
$z_{xx}=\frac{4-4z+z^2+x^2}{(2-z)^3}.$ Вы не могли бы сказать, кто из нас ошибается: книга или я ? Заранее благодарен за Ваше мнение !

[nnosipov]

Evgenii2012 в сообщении #1451463 писал(а):

Вы не могли бы сказать, кто из нас ошибается: книга или я ?

Оба ответа могут быть правильными. Попробуйте ответ из книги свести к Вашему, заменив все степени $z^k$ с $k \geqslant 4$ степенями, меньшими $4$ (используя уравнение, которому удовлетворяет $z$).

Upd. Хотя нет, здесь это не поможет, ответы явно разные. Но у Вас ответ правильный (по крайней мере, у меня получилось так же).

[nnosipov]

Evgenii2012 в сообщении #1451463 писал(а):

У меня получается ответ $z_{xx}=\frac{1-2z+z^2+x^2}{(1-z)^3},$ а в книге ответ
$z_{xx}=\frac{4-4z+z^2+x^2}{(2-z)^3}.$

И здесь Вы правы.

[Evgenii2012]

nnosipov, большое спасибо за Ваше мнение !

[Pphantom]

И, Evgenii2012, не ставьте проценты в таком количестве. За пределами математического тэга движок LaTeX не работает и они видны (сейчас я их поубирал).