Здравствуйте!
Решаю задачу

Будем для определённости искать минимум.
Составим лагранжиан

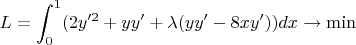
Выпишем уравнение Эйлера-Лагранжа для данного функционала


Далее получим
 И вот тут вопрос.
И вот тут вопрос. В последнее уравнение не вошло число

- можно ли утверждать, что подойдёт любое

?
Далее подставим начальные данные и тогда:

 Проверка условий.
Проверка условий. 
Проверим условие Лежандра: для этого нужно найти

![$$L''_{y'y'}(\widetilde{y}) = 4 > 0 \, \forall x \in [0, 1], \Rightarrow \text{выполнено усиленное условие Лежандра}.$$ $$L''_{y'y'}(\widetilde{y}) = 4 > 0 \, \forall x \in [0, 1], \Rightarrow \text{выполнено усиленное условие Лежандра}.$$](https://dxdy-01.korotkov.co.uk/f/8/2/e/82ef611ca11d088454c6b8ac683aa03382.png)
Проверим условие Якоби: для этого нужно выписать уравнение вида

где

В нашем случае


Собственно, здесь и начинаются вопросы(точнее, они появились уже на поиске экстремали).
1. Здесь остаётся

. Получается, это будет параметр, который и оставлять до ответа? Или же можно подставить какое-то значение?
2. По алгоритму нам далее нужно найти сначала общее решение последнего уравнения с начальными данными

, а затем и частное c начальными данными

. Чему тогда будет равно значение

и как его найти в общем случае?



