Рассмотрим следующую игру. У игроков

,

и

лежит в кошельке
соответственно

,

и

одинаковых монет. Каждый раунд состоит в следующем. Каждый
игрок сначала выбирает одну из имеющихся у него монет и затем все трое одновременно
подбрасывают каждый свою монету. Если две монеты выпали одинаковой стороной,
владельцы этих монет отдают их третьему игроку. Если все монеты выпали одинаковой
стороной, раунд повторяется. Игра продолжается до тех пор, пока у одного из игроков не
закончатся монеты. Чему равно среднее число раундов до окончания игры при

,

,

, если вероятность выпадения орла равна
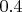
?
Тут система линейных уравнений выходит на средние времена из разных состояний. И количество уравнений огромное - даже с учетом симметрии их выходит 30 штук. Как проще решить, подскажите, пожалуйста!