Число допустимых решений ЗЛП

[Andrey_Kireew]

Доброе утро уважаемые участники. Давно не даёт покоя один вопрос - определение числа допустимых решений ЗЛП. Насколько мне известно, что допустимые решения находятся в вершинах многомерного многогранника. Число таких вершин равно произведению числа ограничений и числа переменных. С другой стороны, используя комбинаторные оценки, получается совсем другое число допустимых решений ЗЛП, которое намного больше и лично мне представляется более правдоподобным. Например, для системы ограничений:

$$\left\{ \begin{array}{rcl} &a_{1,1}x_1+a_{1,2}x_2+a_{1,3}x_3+a_{1,4}x_4>L_1& \\ &a_{2,1}x_1+a_{2,2}x_2+a_{2,3}x_3+a_{2,4}x_4>L_2& \\ &a_{3,1}x_1+a_{3,2}x_2+a_{3,3}x_3+a_{3,4}x_4>L_3& \\ \end{array} \right.$$

число допустимых решений

$$N=\frac{4!}{3!\cdot1!}=4$$

а число вершин многогранника

$$N=4 \cdot 3 =12$$

в общем не совпадает. Может кто нибудь подскажет, в чём у меня ошибка?

[пианист]

Andrey_Kireew в сообщении #1447283 писал(а):

Число таких вершин равно произведению числа ограничений и числа переменных

Почему?

[Andrey_Kireew]

пианист в сообщении #1447332 писал(а):

Почему?

Это приблизительно. Если число ограничений меньше размерности, то пространство не ограничено. Если число ограничений равно n+1 (где n размерность) получается простейший n+1 - аэдр. Далее, каждое новое ограничение даёт n-1 новых вершин. При этом, вершины всё время остаются n валентными, и этот процесс может продолжаться бесконечно.
Получается примерно произведение. Откуда катастрофический рост количества вершин, который по идее должен наблюдаться, я пока понять не могу

[starper]

Andrey_Kireew, насколько я знаю, допустимым решением называют любое, которое удовлетворяет ограничениям, то есть в вашем примере их бесконечно. То, что вы назвали числом допустимых решений - это, похоже, число базисных решений, то есть решений, которые построены на линейно-независимых векторах, которые образуют базис пространства условий. А число вершин многогранника - это число угловых точек из пространства решений, (угловые точки - те, которые не могут быть выражены, как выпуклая комбинация векторов из пространства решений), они не могут иметь больше, чем m ненулевых координат (m - размерность пространства условий), но может быть меньше, чем m, поэтому число вершин многогранника больше чем число базисных решений.

[Andrey_Kireew]

starper в сообщении #1447440 писал(а):

То, что вы назвали числом допустимых решений - это, похоже, число базисных решений, то есть решений, которые построены на линейно-независимых векторах, которые образуют базис пространства условий

можно сказать и так

starper в сообщении #1447440 писал(а):

поэтому число вершин Многогранника больше чем число базисных решений

как же так? всё должно быть наоборот, как я понимаю число, базисных решений - это число возможных комбинаций векторов условий в базисе, оно находится через факториалы и очень велико, а число вершин - это просто произведение размерности и числа ограничений. Или может я что то неверно понимаю?

[starper]

Andrey_Kireew в сообщении #1447491 писал(а):

как я понимаю число, базисных решений - это число возможных комбинаций векторов условий в базисе, оно находится через факториалы и очень велико, а число вершин - это просто произведение размерности и числа ограничений. Или может я что то неверно понимаю?

Первое верно, а про число вершин как произведение это откуда факт? Базисные решения -тоже вершины многогранника из пространства решений. Но только кроме базисных решений есть ещё вершины.

[Andrey_Kireew]

starper в сообщении #1447513 писал(а):

а про число вершин как произведение это откуда факт?

вот откуда

Andrey_Kireew в сообщении #1447394 писал(а):

Если число ограничений меньше размерности, то пространство не ограничено. Если число ограничений равно n+1 (где n размерность) получается простейший n+1 - аэдр. Далее, каждое новое ограничение даёт n-1 новых вершин. При этом, вершины всё время остаются n валентными, и этот процесс может продолжаться бесконечно

я пришел к такому умозаключению.
Например берём треугольник на плоскости. Каждое линейное ограничение добавляет максимум 1 новую вершину, и это в лучшем случае. Берём тетраэдр - каждое новое линейное ограничение добавляет 2 вершины, опять же в лучшем случае.
Я предполагаю, что в любом n-мерном случае будет та же картина. А если так, то число вершин не может так сильно расти.
Где ошибка в моих рассуждениях?

[starper]

Andrey_Kireew в сообщении #1447394 писал(а):

Если число ограничений меньше размерности, то пространство не ограничено.

Не факт, кстати, если, например в вашей системе все коэффициенты $a_i_j$ отрицательны, то уже точно будет ограниченным

-- 26.03.2020, 23:13 --

Andrey_Kireew в сообщении #1447394 писал(а):

Если число ограничений равно n+1 (где n размерность) получается простейший n+1 - аэдр.

И в этом случае может неограниченное множество получиться, все зависит от коэффициентов в системе

[Andrey_Kireew]

starper в сообщении #1447565 писал(а):

И в этом случае может неограниченное множество получиться, все зависит от коэффициентов в системе

может, но больше n+1 вершин не получить никак, вот в чём дело

[starper]

Andrey_Kireew, я понял, что вы имеете в виду. Но для двух и трехмерного пространства ваши оценки и комбинаторные совпадают. Значит в более высоких размерностях по-другому происходит. Тоже стало интересно почему, думать надо

-- 27.03.2020, 02:37 --

Например, для трехмерного пространства 3 гиперплоскости могут высечь куб, т. е. 8-вершинник. Для 4-мерного 4 гиперплоскости 16-вершинник могут высечь, для пятимерного уже 32 и т.д., то есть уже для пятимерного пространства оценка одно ограничение - не больше n+1 вершины не работает

[Andrey_Kireew]

starper в сообщении #1447587 писал(а):

Например, для трехмерного пространства 3 гиперплоскости могут высечь куб

в трёхмерном пространстве они не гипер - а просто плоскости, и трёх - недостаточно, чтобы образовать куб, нужно 6 штук, это я могу представить. Если потом его дробить, так как я раньше описывал, срезая вершины, то каждая новая плоскость будет давать так же 2 новые вершины. Все вершины так и остаются трёхвалентными. И вообще, при срезании вершины любой валентности, новые вершины станут трёхвалентными. И грани, по большей части будут все треугольные. Ну в 3D графике так ведь и есть - все грани у каких угодно сложных фигур треугольные.
Да и не только куб, могут и более сложные фигуры высечь, но число вершин, приходящееся на одну плоскость будет меньше, чем в случае с тетраэдром. Я же рассматриваю случай с максимально возможным числом вершин.

Пространства более высокой размерности, в силу ряда причин, я не могу себе так хорошо представить. Всё это находится за гранью человеческого понимания. Остаётся лишь сетовать на какие то формальные закономерности.

Вот например, из теоремы Эйлера для выпуклого многогранника следует:

$$V=2+R-G $$

число граней G - это и есть число ограничений, а число рёбер R - равно половине произведения числа вершин и их валентности (которая равна размерности пространства Size).
Получаем:

$$V=(G-2)/ (Size/2-1)$$

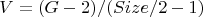
это вообще кошмар какой то, хотя, для тетраэдра и для куба работает. Вообще, есть серьёзные подозрения, что теорема Эйлера справедлива лишь для трёхмерного пространства. Видимо, он так и не смог до конца постичь этой тайны.

Об этом косвенно свидетельствует и тот факт, что работы Эйлера пытались обобщить, в частности Пуанкаре, в википедии даже приводится какая то странная формула, но что конкретно она обобщает, я так к сожалению и не понял. В том смысле, что неясно как по ней вычислить количество вершин N-мерного многогранника.

[ИСН]

Andrey_Kireew в сообщении #1447614 писал(а):

Вообще, есть серьёзные подозрения, что теорема Эйлера справедлива лишь для трёхмерного пространства.

"Есть подозрение, что ходить ногами можно только по поверхности." Разумеется, а как ещё-то? В каком ещё пространстве есть все эти объекты, из которых состоит формулировка теоремы, и только они?

Есть обобщение на любые размерности, известно давно. Оно формулируется не сложнее, чем для 3D. Скажем, для размерности 4: N(вершин) - N(рёбер) + N(граней) - N(гиперграней) = 0.

[Andrey_Kireew]

ИСН в сообщении #1447615 писал(а):

гиперграней

уточните, какой смысл Вы вкладываете в понятие "гипергрань" чтобы можно было воспользоваться этой формулой

[ИСН]

В данном случае - трёхмерная грань четырёхмерного тела.

[starper]

Andrey_Kireew в сообщении #1447614 писал(а):

starper в сообщении #1447587 писал(а):

Например, для трехмерного пространства 3 гиперплоскости могут высечь куб

в трёхмерном пространстве они не гипер - а просто плоскости, и трёх - недостаточно, чтобы образовать куб, нужно 6 штук, это я могу представить.

Ну я имел в виду для нашей задачи, в ЗЛП же условие неотрицательности на переменные установлено и получается, что $n$ гиперплоскостей это условие дает, и еще $n$ ограничений дают нам новые гиперплоскости.

-- 27.03.2020, 11:45 --

В нашей задаче гиперграни высекают ограничения, если заменить неравенства на равенства. Например, единичный 4-куб получился бы, если бы гиперплоскости высекли бы множество с вершинами вида $(1, 0, 0, 0), (1, 1, 0, 0) $ и т. д., всего 2^4 вершин. 3-мерные грани получаются как множества, натянутые на 8 точек (только таких, чтобы их выпуклые комбинации не попадали внутрь 4-куба)