Вопрос
В окружность с центром

вписано правильный многоугольник, показать что половина стороны этого многоугольника будет бесконечно малой величиной если количество сторон постоянно увеличивать.
Попытки разобраться с решением
Не особо понятный момент почему всегда выполняется неравенство

, допустим мы запишем угол

, а дальше через этот угол посчитаем разность, а именно

превратим это в функцию

и нарисуем ее график, для красоты сверху еще график функции синуса дорисуем.
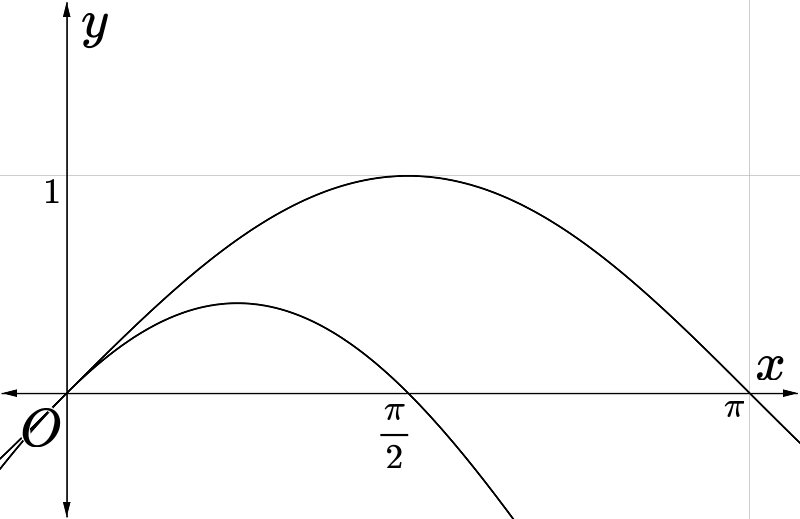
Правильно ли я довел что неравенство для треугольника

всегда выполняется?



