arseniivА, все, представил. Правильно вроде. Однозначно задать движение абсолютно твердого тела можно ток тремя точками. Довольно абстрактно вообще-то, вся суть как мне кажется в связях, ведь чтобы задать движение точки, достаточно точки, чтобы задать движение, всевозможные, бесконечно тонкого отрезка, достаточно двух точек и их движений, а для твердого тела которое складывается с множества точек, достаточно трех.
amonНа счет рисунка, не проблема, я могу нарисовать детально если показать мне как. В любом случае это лично мне надо разбираться со всем этим чтобы понять вращение.
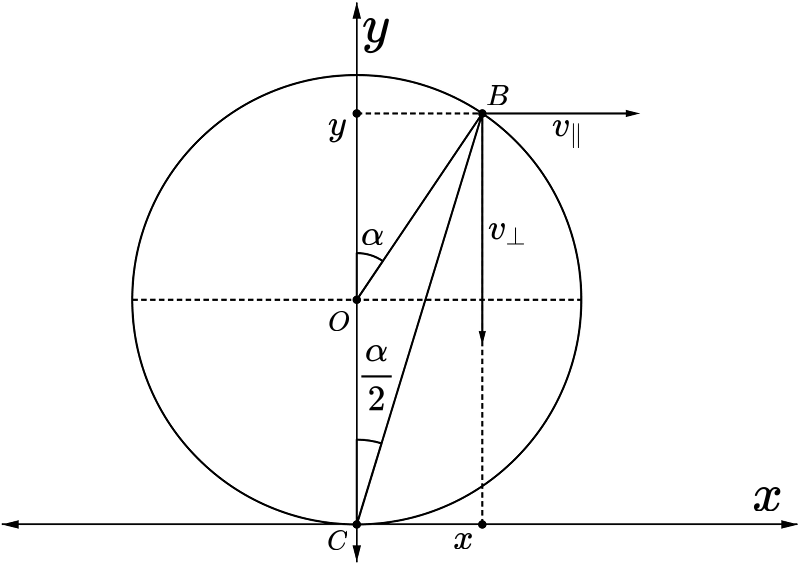
Поскольку треугольник на рисунке равнобедренный, стороны как радиусы, можно напечатать что

, используя радианы запишем всем известную формулу для угловой скорости

. Теперь запишем вертикальную составляющую скорости точки

, а именно я не совсем понял откуда оно взялось, ведь скорость то не просто кручение а еще движение вперед, то есть относительно неподвижной системы отсчета будет
![$\overrightarrow{v} = \overrightarrow{v_{O}} + \left[\overrightarrow{\omega}, \overrightarrow{R}\right]$ $\overrightarrow{v} = \overrightarrow{v_{O}} + \left[\overrightarrow{\omega}, \overrightarrow{R}\right]$](https://dxdy-04.korotkov.co.uk/f/3/b/c/3bc817baaefab5f368c54c52ef9f471a82.png)
. А не, решил не удалять ход своих мыслей, все правильно, скорость центра колеса не влияет никак на вертикальную скорость ибо оно горизонтальное, хотя все ровно не понял почему когда колесо движется у нас тоже уравнение что и для неподвижного... Ладно, разберусь.
realeugeneЯ что-то неприпомню чтобы говорил тут за интуицию, ну ладно, оно действительно у меня своеобразное...

На счет бесконечно малых, как-раз недавно прошел эту тему сразу после гипербол и парабол с эллипсами по книге для техникумов, пару месяцев назад. Поэтому пока еще не забыл, и без подглядываний сразу скажу что бесконечно малые это переменные величины, такие что, какое бы мы не выбрали постоянное число, то его абсолютная величина будет больше чем такое же в бесконечно малой. На счет рядов, вот тут то плохо, еще не изучал заново, но буду по книге для техникумов! А потом по Фихтенгольцу закреплю.
Когда-то давно-давно был у меня спецкурс, на который я естественно не ходил почти, называлось
асимптотические методы в математической физике, вроде так. Так вот в теории эти Тейлоры, Маклорены и Фурье хороши, и позволяют складывая некие кусочки в которые не входят функции в явном виде, а лишь аргумент в той точке и производные там же, получить бесконечно точное приближение значения функции там или сям, но на деле, походу все достаточно плохо, и функции должны быть такие-эдакие чтобы эти ряды работали, и не сложные особо ибо и компьютер зависнет, и еще что-то, в общем не помню...