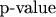В теме по корона вирус (
от этого сообщения и несколько выше) с уважаемым
Dmitriy40 возникла дискуссия на тему "можно ли оценивать уровень смертность от вируса, как отношение умерших к количеству случаев - по всей статистике из Китая, за исключением очага (провинции Хубей)?".
Я считаю, что - можно.
Нужно отметить, что в Китае в больницах остается уже меньше

от зараженных, а в вне очага примерно

, то есть (на мой взгляд) статистику можно считать собранной. Искажения из-за отставания количества умерших от количества зараженных уже будут небольшими.
Был выдвинут другой контраргумент - большой разброс коэффициента смертности, посчитанной по каждой провинции в отдельности, что (как я понял контр аргумент) говорит о недостаточности статистики (а это около 13 тысяч случаев).
Ниже в нескольких сообщениях (скажу, когда будет последнее) будет описание моих расчетов, с попыткой опровергнуть этот контраргумент.
Просьба - оценить, насколько это всё адекватно
 -- 12.03.2020, 18:11 --
-- 12.03.2020, 18:11 --1.
ДатасетДатасет был взят с
известного китайского сайта.
Вроде бы за 10 марта, но может и за 11 марта (что-то не отследил, они уже обновились сегодня или нет, когда забирал данные).
По каждой провинции имеются данные об общем количестве случаев (

- в таблицах, которые будут ниже), и о количестве умерших (

)
UPD: кроме данных по провинциям материкового Китая там есть данные по Гонконгу, Макао и Тайваню. Их тоже забрал
-- 12.03.2020, 18:18 --2. Модель \ нулевая гипотеза1. Предполагается такой процесс: человек заболевает и с какой-то постоянной вероятностью умирает.
2. Тогда количество умерших при известном количестве заболевших будет описываться биноминальным распределением.
2а. В таблицах будут колонки и с распределением Пуассона, но результат практических не отличается от биноминального распределения.
3. Вероятность умереть оценивается как отношение количества умерших к количеству заболевших, суммарно по всем провинциям
4. Нулевая гипотеза - коэффициент смертности одинаков во всех провинциях и равен оценке (п.3 выше).
-- 12.03.2020, 18:37 --3. Расчет 
1. По определению

- вероятность, что статистика (в данном случае - количество умерших, при известном количестве заболевших и при оцененном коэффициенте смертности) имеет наблюдаемой значение или более экстремальное.
2. Рассчитывалось (Экселем

)

, где

- вероятность, что значение количества умерших будет таким же, как наблюдается (

) или меньше.

- функция распределения вероятности для биноминального распределения.
3. Рассчитывалось


- вероятность, что значение количества умерших будет таким же, как наблюдается (

) или больше.

- вероятность того, что значение будет ровно таким, как наблюдается. Так как распределение дискретное, эту поправку нужно учитывать.
4. Рассчитывалось
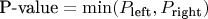
5. Для двусторонней оценки

рекомендуют использовать

. Но там нужно ещё немного поприседать с поправками на дискретное распределение. Что я и сделал позже. Особо на результаты не повлияло. Эти расчеты выкладывать не буду.
-- 12.03.2020, 18:50 --4. Выбор критерия статистической значимости и поправки на множественную проверку гипотез.
1. Критерий выбран стандартный -

2. Так как проверяем не одну нулевую гипотезу, а много - по одной на каждую. провинцию, а их много (около 30), то требуются поправки на множественности гипотез.
3. Поправки считались по трем методам:
а) Метод Холма (поправка Холма — Бонферрони)
б) Метод Шидака-Холма
в) Метод Бенджамини — Хохберга
подробности, достаточные для их применения, можно почитать
тут.
Первые две поправки почти одинаковы и на практике не различаются. Метод Бенджамини — Хохберга более жесткий к гипотезам с небольшим