Если немного подкоректировать немного неправильную в плане коэффициентов функцию разброса, и учесть слагаемые с

, в результате будет что-то такое

Нарисовав соответствующий график ниже мы получим некую быстро взмывающую вверх линию опять...

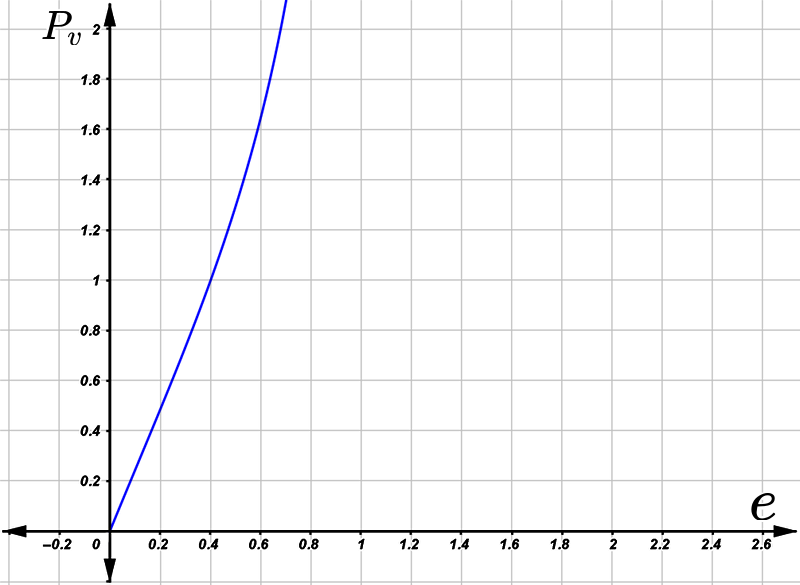
Чего как-бы и не должно быть. Например выберем планету солнечной системы нашей, а именно Меркурий. У нас будет


что в общем то похоже по идее на истину, теперь тоже самое для минимальной скорости Меркурия


Но кроме эллиптический орбитальных скоростей нам нужна еще и круговая, вот тут и была найдена ошибка в формулах в тетради! Круговой радиус орбиты Меркурия оказался больше размера главной полуоси эллипса орбиты. Капец...

Уже второй раз так путаю фокус и главную полуось, первый был в простенькой задачи которую долго не мог решить и не понимал почему ответы не совпадают. Можно было выше это все не печатать, но мне жаль было стирать столько Латеху.
Да найдем же новый, верный круговой радиус!

Соответственно и новая формула для круговой скорости

с которой тут же получается выражение для разброса

и нарисуем ка мы график разброса в зависимости от эксцентриситета...
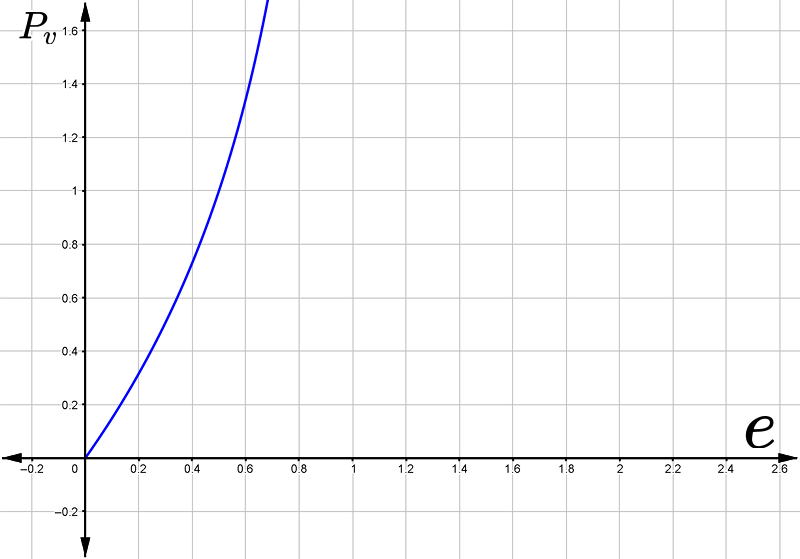
Опять что-то не то что ожидалось. Может апроксимацию неправильную выбрал? Разлет в скоростях для Меркурия получается по

за графиком, это конечно много. А как это численно будет

значения разброса в процентах для Меркурия

Либо сначала неправильно апроксимировал эллипс окружностью, либо таки правда, что разлет в скоростях, а следовательно неравномерность движения будет большая и расти будет с огромной скоростью когда эксцентриситет эллиптической орбиты приближается к единице, надо бы посчитать сколько на единицу длины получиться разброс в среднем. Черт, наверное ошибся в рассуждениях, ну ладно, подумаю... Мож не ту скорость взял, надо было среднюю какую-то? Но как связать среднюю скорость с кругом и эллипсом?
А пока я понял, по идее, что:
- на самом деле мы могли площадь треугольника взять "с потолка", как аксиому, если бы наперед знали ее с математического анализа;
- формулу в книге можно воспринимать просто как результат неких математических действий, которые мы потом использовали в физической модели а не как формулу которая получалась с физической модели;
- без математического анализа физическую модель эллиптической орбиты и второго закона Кеплера не так то просто построить, круговые приближения не проходят, слишком огромная неравномерность.
DimaMИнтересная формула кстати, буду разбираться! Пока не особо понятная...
wrestНу да, наверное так проще представить свободное движение спутника там какой-то планеты под действием силы тяжести. Но я просто подумал что не увеличивается же скорость когда расстояние возрастает в случае эллиптической орбиты.