Определение изоморфизма

[Someone]

oleg.k в сообщении #1441846 писал(а):

А групп две.

А формальная теория под названием "группа" — одна. Просто у неё много интерпретаций.

oleg.k в сообщении #1441846 писал(а):

Далее в книге говорилось, что с логической точки зрения подстановка терма $t$ вместо $x$ в формулу $A$ является правильной и осмысленной, только если $t$ свободен для $x$ в $A$.

Я об этом и пишу. Именно поэтому нужно либо различать "локальные" и "глобальные" переменные, либо переименовывать переменную в области действия квантора, чтобы её имя ни с чем не совпадало. Как я писал, математики предпочитают второй подход.

arseniiv в сообщении #1441840 писал(а):

Ну да, именно высказывания об элементах только одной группы.

Да, теория, называемая "группа", говорит только об одной группе. Но любой. А то, что называется "теория групп" — это метатеория для теории "группа". И обсуждаются в ней всевозможные интерпретации теории "группа".

[arseniiv]

oleg.k в сообщении #1441846 писал(а):

Замена - это подстановка?

Ага.

oleg.k в сообщении #1441846 писал(а):

Далее в книге говорилось, что с логической точки зрения подстановка терма $t$ вместо $x$ в формулу $A$ является правильной и осмысленной, только если $t$ свободен для $x$ в $A$. Это я все к тому, что получается очень прозрачная картина.

Говорить об отдельных вхождениях конечно же полезно, это я не отрицаю. А вот сама нужда определять свободу для подстановок показывает, что соответствующий уровень формализации низковат. И если например требовать чтобы каждый квантор во вселенной связывал свою уникальную переменную, отличную кроме того от всех свободных переменных, которые нам попадутся, окажется, что мы наконец можем подставлять что угодно куда угодно и не связать ненароком исходно свободные вхождения. (Индексы де Брёйна дают другой способ с этим сладить — грубо говоря, автоматизировать распределение «достаточно уникальных» имён связанных переменных.)

oleg.k в сообщении #1441846 писал(а):

А групп две. И что значит вот это "любое утверждение" из цитаты Винберга мне непонятно. Может тут речь идет о том, что есть две разные алгебраические структуры, 2 формальные теории, 2 интерпретации и какой-то крутой логикоматематический финт, который с помощью индуктивного характера определения термов и формул позволяет поставить какое-нибудь взаимно-однозначное соответствие между формулами из двух разных формальных теорий при изоморфизме этих структур...

Есть. Пусть мы рассматриваем язык и структуры одной и той же сигнатуры. Назовём теорией $T(\mathcal S)$ структуры $\mathcal S$ множество всех замкнутых формул языка, истинных в этой структуре. Тогда во-первых $\mathcal S$ — модель $T(\mathcal S)$, во-вторых $T(\mathcal S)$ — теория полная и непротиворечивая — т. е. в результате это «самая хорошая теория, описывающая $\mathcal S$», — и в-третьих если $\mathcal S_1\cong\mathcal S_2$, то $T(\mathcal S_1) = T(\mathcal S_2)$. Вот это оно и есть; последнее равенство называется элементарной эквивалентностью $\mathcal S_1$ и $\mathcal S_2$, и на всякий случай в обратную сторону оно кстати не работает (две элементарно эквивалентные структуры не обязательно изоморфны).

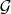
(С учётом предыдущего поста Someone: для группы $\mathcal G$, $T(\mathcal G)$ будет расширением теории «группа», то есть вторая входит в первую (как множество формул). И $\mathcal S$ — модель теории $\mathcal T$, если и только если $\mathcal T\subset T(\mathcal S)$; так это всё соединяется воедино.)