SomeoneИспользуем формулу из Википедии для приближенного вычисления скорости тела на эллиптической орбите в какой-то момент времени

где

— масса Солнца умноженная на гравитационную постоянную в системе СИ,

— расстояние от фокуса где Солнце до объекта,

— длина главной полуоси эллиптической орбиты. Разберусь когда-то с этой формулой, как-раз кстати по теме законов сохранения, второго закона Кеплера и закона всемирного тяготения Ньютона, да и интересно. Из соображений эллиптичности, максимальна скорость будет при минимальном расстоянии к Солнцу, а минимальная при максимальном. С этого сразу запишем разброс скорости

вспоминая наши прошлые обозначения и рисунок эллипса, выразим максимальные и минимальные расстояния через эксцентриситет и главную полуось


Апроксимируем эллипс кругом, как на рисунке.
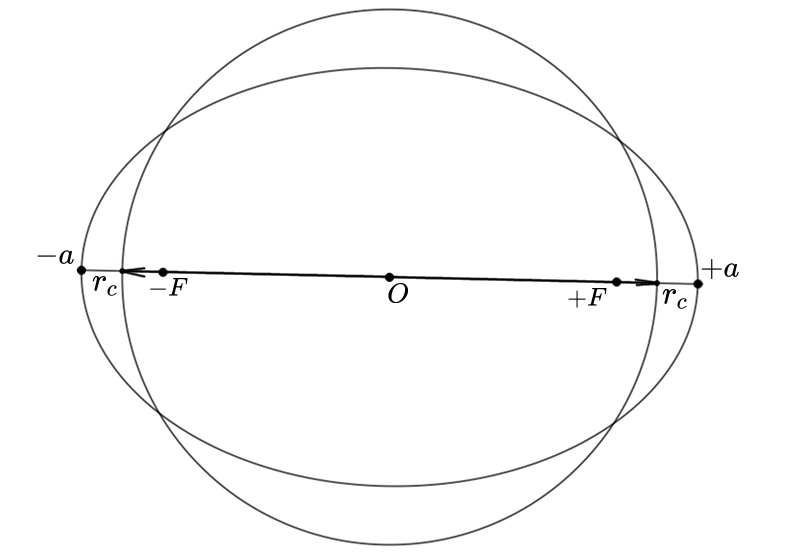
Запишем для него орбитальную скорость исходя со второго закона Ньютона и закона всемирного тяготения того же человека, для этого выберем радиус эллипса таким что

соответственно выражение для постоянной скорости кругового орбитального движения будет

Разделим разброс скорости эллиптического орбитального движения на постоянную скорость кругового, чтобы узнать насколько эллиптичность разбрасывает скорость

отбрасывая покамест все что умножается на эксцентриситет в квадрате, получаем

По крайней мере будет как-то работать пока

, кстати в формулу не входит в явном виде малая полуось, видать результат апроксимации что делалось в выражении для эллиптической скорости что было взято с Википедии. Коэффициент

тоже интересен. Теперь нужно посмотреть сколько процентов разброса в скорости припадает на некую единицу длины эллиптической орбиты в среднем. Для этого надо бы найти длину эллипса, поэтому воспользуемся формулой некого Сриванаса Рамануджаны:

где

и

есть большая и малая полуось эллиптической орбиты. Но проблема в том что у нас есть только основная полуось и эксцентриситет, поэтому посмотрев на определения эллипса в собственных координатах придется выразить меньшую полуось как

Перепишем соответствующую формулу

вообщем незнаю уже упростить эту формулу, думаю пора заняться счетом, так как размерности совпадают более-менее. Запишем некоторую величину

оно и будет характеризовать средний эллиптический разброс скоростей и соответственную неравномерность движения в сравни с случаем круговой орбиты в процентах на единицу длины

нужно еще нарисовать график функции отношения разброса к круговой постоянной скорости в зависимости от эксцентриситета, хотя конечно опять непонятно почему не всчитывается малая полуось, это правда может быть следствие закона равных площадей отсекаемых для центральной силы.
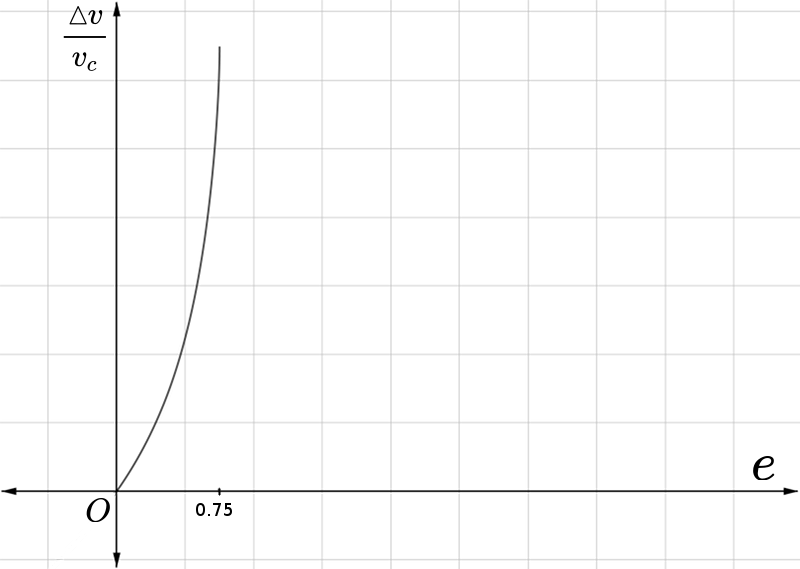
Что-то не то получилось...

Не должно так быстро расти этот разброс, смысл был в том чтобы доказать что разброс растет медленно и что можно использовать круг когда надо. Ладно, уже глаза устали, потом разберусь.
miflinТо есть, в пункте два мы прилепливаем основание треугольника к эллипсу считая окружностью или оно прилепливается к пустому пространству как в случае с секторами? Вообще не понял использования

, и причем здесь парабола?
svvДа это я знаю, что надо учить математический анализ, но у меня плохо получается. Там кстати пропущенное слагаемое в длинной дроби —

, смысл был в том, что у себя в тетради я проделал формульные расчеты и получилось что смог выразить сразу-же, без явного математического анализа приближенную формулу для изменения косинуса угла пустого фокуса

, и потом мне удалось подсчитать там численно и что-то сказать в своей дискуссии с тем человеком, но запечатлив это в Латехе я вдруг понял что ошибся где-то в конце и неполучиться там так как я думал с самого начала.
А терять время, это да... Это мы умеем к сожалению лучше всего по ходу действия и по жизненной истории, ну хотя с другой стороны, в терянии времени и плохого особо ничего нету со взгляда высокоморального, минус в том что также нету никакого дохода денежнего.