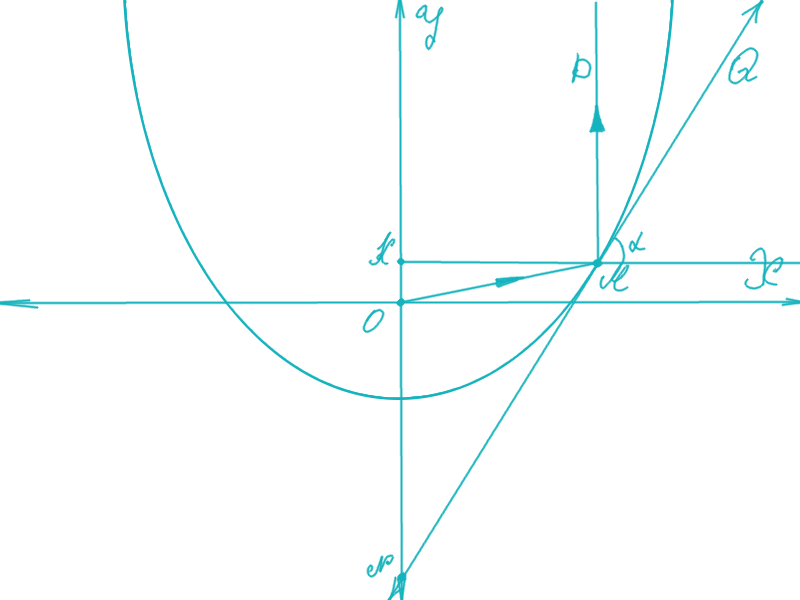
Луч света идет от источника точки

, попадает в

, отражается на зеркальной поверхности, и движется дальше, причем мы считаем луч после отражения параллельный оси ординат. Точка

имеет координаты

. Из-за закона отражения

, а также

, как созданные параллельными прямыми, в результате

— равнобедренный. С треугольника

находим тангенс угла

, который равен углу

как вертикальные углы.

и таким образом

но
откуда получается вот это?

В смысле я понимаю геометрический смысл производной, но я не пойму откуда то что справа после знака равно образовалось, с рисунка не понять так сразу что-то... Книга "Рассказы о прикладной математике", Тихонов, Костомаров, страницы 176 — 178, а и еще одно, у меня там на рисунке не видно что

, но они вообще должны быть равны. Спасибо за ответы.



