База топологии это такое семейство

открытых в

множеств, что каждое открытое в

множество является объединением некоторой совокупности множеств из

.
Это правильно.
В пункте 3) я подразумевал, что объединение(все возможные варианты объединений) конечного количества подмножеств

дадут множество подмножеств такого же типа как

.
3)

.
Я не вижу здесь "всех возможных вариантов объединения". В левой части стоит нечто похожее на объединение подмножеств множества

(меня смущает запись

вместо просто

; где-то рядом должно быть написано, что

или сказано то же самое словами). Известно, что объединение подмножеств

тоже является подмножеством

, но в правой части вместо этого написано какое-то семейство интервалов. Между тем, здесь объединение явно вычисляется. Попробуйте представить себе геометрически объединяемые множества и их объединение. А также рассмотрите и объединения бесконечных подсемейств семейства

.
Есть множество
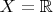
. Есть подмножество множества

. Вопрос: является ли семейство подмножеств

базой некоторой топологии на

.
Слово "некоторой", видимо, надо интерпретировать так, что эта топология не обязана совпадать со стандартной топологией множества действительных чисел.
Кстати, почему ваше семейство

не является базой стандартной топологии

?
Для решения вашей задачи есть удобный критерий того, что произвольное заданное семейство подмножеств некоторого множества

является базой какой-нибудь топологии на этом множестве. Если этого критерия Вы не изучали, то в данном случае можно легко описать все множества, принадлежащие искомой топологии, и убедиться, что семейство

является базой этой топологии.



